Efficient Residue Number System Based Winograd Convolution
Paper and Code
Jul 23, 2020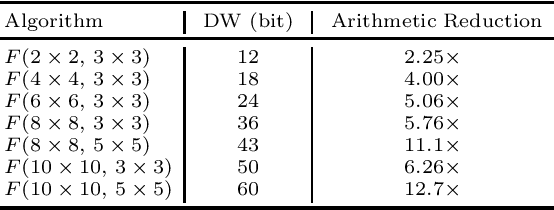
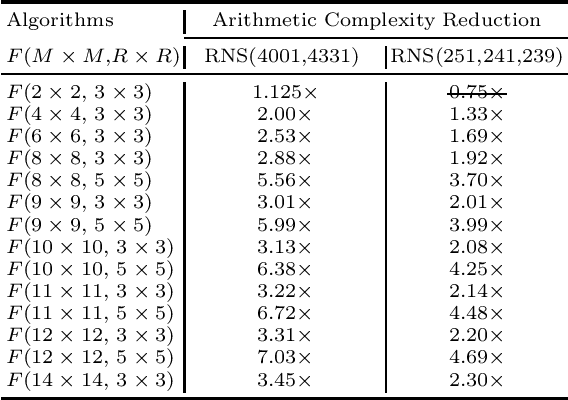
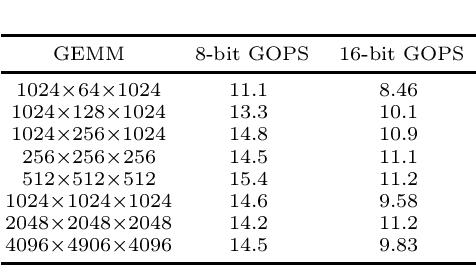
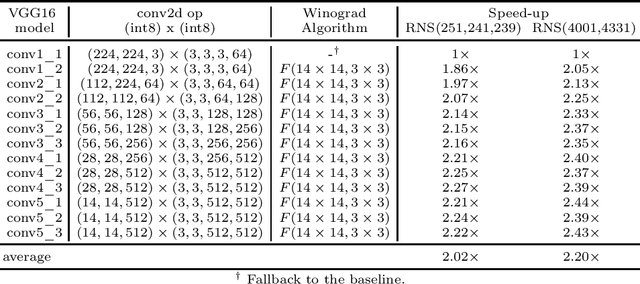
Prior research has shown that Winograd algorithm can reduce the computational complexity of convolutional neural networks (CNN) with weights and activations represented in floating point. However it is difficult to apply the scheme to the inference of low-precision quantized (e.g. INT8) networks. Our work extends the Winograd algorithm to Residue Number System (RNS). The minimal complexity convolution is computed precisely over large transformation tile (e.g. 10 x 10 to 16 x 16) of filters and activation patches using the Winograd transformation and low cost (e.g. 8-bit) arithmetic without degrading the prediction accuracy of the networks during inference. The arithmetic complexity reduction is up to 7.03x while the performance improvement is up to 2.30x to 4.69x for 3 x 3 and 5 x 5 filters respectively.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge