Efficient Representative Subset Selection over Sliding Windows
Paper and Code
Sep 03, 2018
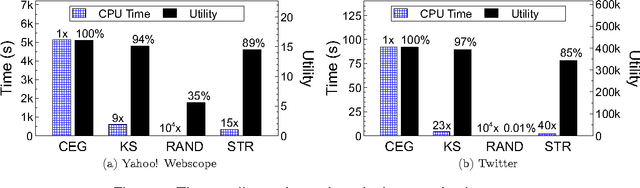
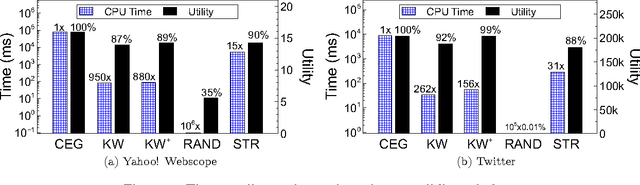
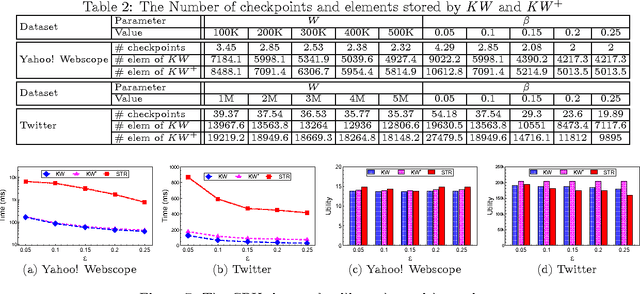
Representative subset selection (RSS) is an important tool for users to draw insights from massive datasets. Existing literature models RSS as the submodular maximization problem to capture the "diminishing returns" property of the representativeness of selected subsets, but often only has a single constraint (e.g., cardinality), which limits its applications in many real-world problems. To capture the data recency issue and support different types of constraints, we formulate dynamic RSS in data streams as maximizing submodular functions subject to general $d$-knapsack constraints (SMDK) over sliding windows. We propose a \textsc{KnapWindow} framework (KW) for SMDK. KW utilizes the \textsc{KnapStream} algorithm (KS) for SMDK in append-only streams as a subroutine. It maintains a sequence of checkpoints and KS instances over the sliding window. Theoretically, KW is $\frac{1-\varepsilon}{1+d}$-approximate for SMDK. Furthermore, we propose a \textsc{KnapWindowPlus} framework (KW$^{+}$) to improve upon KW. KW$^{+}$ builds an index \textsc{SubKnapChk} to manage the checkpoints and KS instances. \textsc{SubKnapChk} deletes a checkpoint whenever it can be approximated by its successors. By keeping much fewer checkpoints, KW$^{+}$ achieves higher efficiency than KW while still guaranteeing a $\frac{1-\varepsilon'}{2+2d}$-approximate solution for SMDK. Finally, we evaluate the efficiency and solution quality of KW and KW$^{+}$ in real-world datasets. The experimental results demonstrate that KW achieves more than two orders of magnitude speedups over the batch baseline and preserves high-quality solutions for SMDK over sliding windows. KW$^{+}$ further runs 5-10 times faster than KW while providing solutions with equivalent or even better utilities.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge