Efficient Global Multi-object Tracking Under Minimum-cost Circulation Framework
Paper and Code
Nov 02, 2019
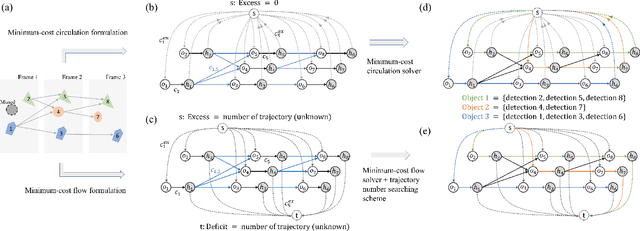

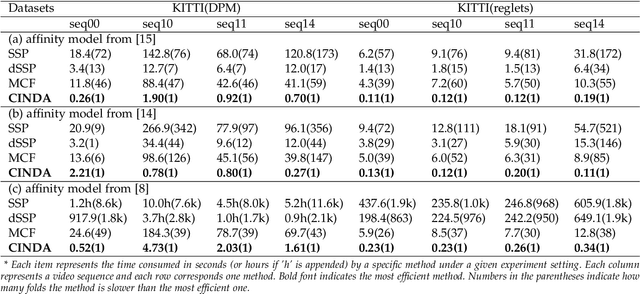
We developed a minimum-cost circulation framework for solving the global data association problem, which plays a key role in the tracking-by-detection paradigm of multi-object tracking. The global data association problem was extensively studied under the minimum-cost flow framework, which is theoretically attractive as being flexible and globally solvable. However, the high computational burden has been a long-standing obstacle to its wide adoption in practice. While enjoying the same theoretical advantages and maintaining the same optimal solution as the minimum-cost flow framework, our new framework has a better theoretical complexity bound and leads to orders of practical efficiency improvement. This new framework is motivated by the observation that minimum-cost flow only partially models the data association problem and must be accompanied by an additional and time-consuming searching scheme to determine the optimal object number. By employing a minimum-cost circulation framework, we eliminate the searching step and naturally integrate the number of objects into the optimization problem. By exploring the special property of the associated graph, that is, an overwhelming majority of the vertices are with unit capacity, we designed an implementation of the framework and proved it has the best theoretical complexity so far for the global data association problem. We evaluated our method with 40 experiments on five MOT benchmark datasets. Our method was always the most efficient and averagely 53 to 1,192 times faster than the three state-of-the-art methods. When our method served as a sub-module for global data association methods using higher-order constraints, similar efficiency improvement was attained. We further illustrated through several case studies how the improved computational efficiency enables more sophisticated tracking models and yields better tracking accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge