Efficient Evaluation of the Number of False Alarm Criterion

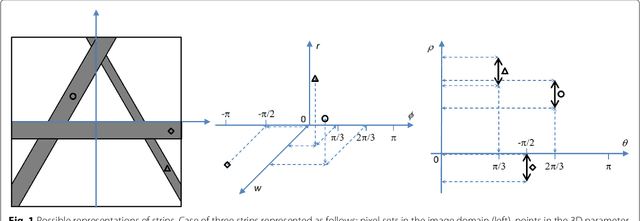
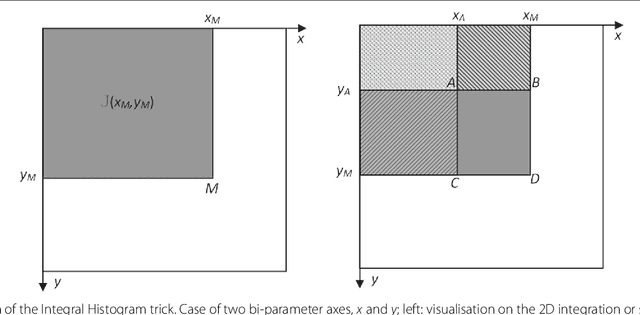
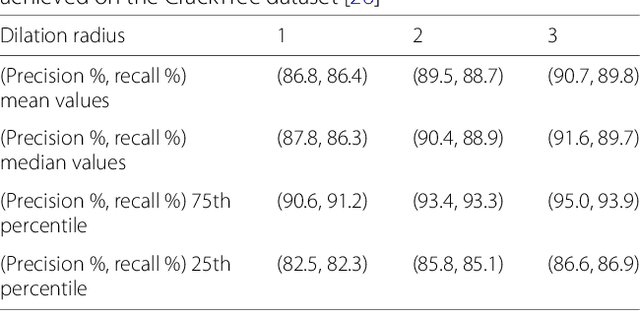
This paper proposes a method for computing efficiently the significance of a parametric pattern inside a binary image. On the one hand, a-contrario strategies avoid the user involvement for tuning detection thresholds, and allow one to account fairly for different pattern sizes. On the other hand, a-contrario criteria become intractable when the pattern complexity in terms of parametrization increases. In this work, we introduce a strategy which relies on the use of a cumulative space of reduced dimensionality, derived from the coupling of a classic (Hough) cumulative space with an integral histogram trick. This space allows us to store partial computations which are required by the a-contrario criterion, and to evaluate the significance with a lower computational cost than by following a straightforward approach. The method is illustrated on synthetic examples on patterns with various parametrizations up to five dimensions. In order to demonstrate how to apply this generic concept in a real scenario, we consider a difficult crack detection task in still images, which has been addressed in the literature with various local and global detection strategies. We model cracks as bounded segments, detected by the proposed a-contrario criterion, which allow us to introduce additional spatial constraints based on their relative alignment. On this application, the proposed strategy yields state-of the-art results, and underlines its potential for handling complex pattern detection tasks.