Efficient Cross-Validation for Semi-Supervised Learning
Paper and Code
Feb 13, 2019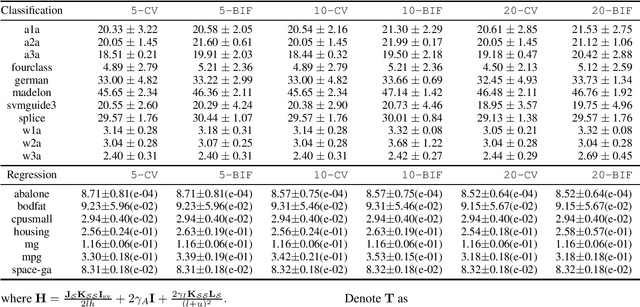
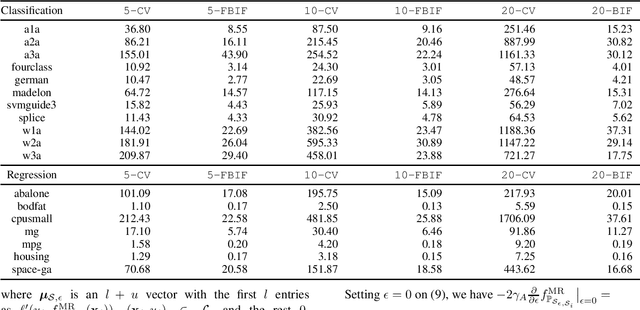
Manifold regularization, such as laplacian regularized least squares (LapRLS) and laplacian support vector machine (LapSVM), has been widely used in semi-supervised learning, and its performance greatly depends on the choice of some hyper-parameters. Cross-validation (CV) is the most popular approach for selecting the optimal hyper-parameters, but it has high complexity due to multiple times of learner training. In this paper, we provide a method to approximate the CV for manifold regularization based on a notion of robust statistics, called Bouligand influence function (BIF). We first provide a strategy for approximating the CV via the Taylor expansion of BIF. Then, we show how to calculate the BIF for general loss function,and further give the approximate CV criteria for model selection in manifold regularization. The proposed approximate CV for manifold regularization requires training only once, hence can significantly improve the efficiency of traditional CV. Experimental results show that our approximate CV has no statistical discrepancy with the original one, but much smaller time cost.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge