Efficient approximation of Jacobian matrices involving a non-uniform fast Fourier transform (NUFFT)

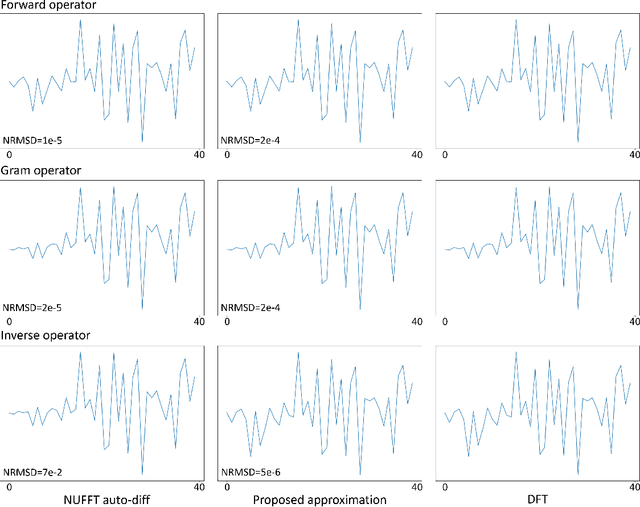
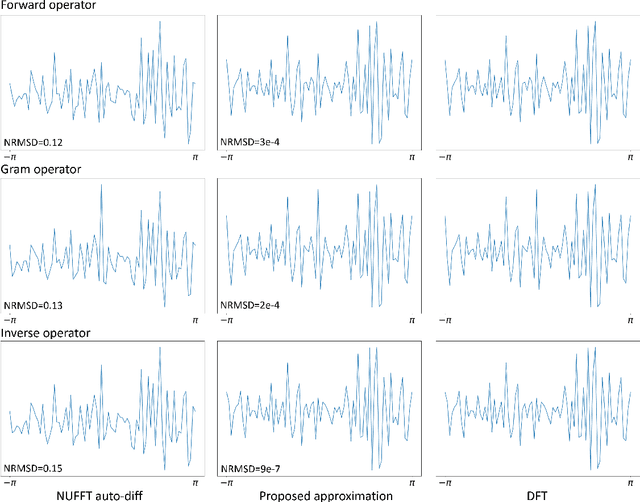
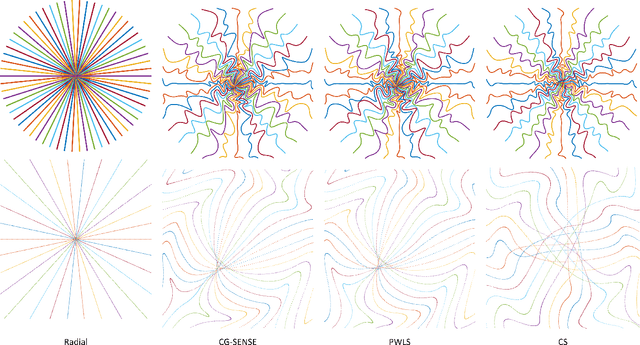
There is growing interest in learning k-space sampling patterns for MRI using optimization approaches. For non-Cartesian sampling patterns, reconstruction methods typically involve non-uniform FFT (NUFFT) operations. A typical NUFFT method contains frequency domain interpolation using Kaiser-Bessel kernel values that are retrieved by nearest neighbor look-up in a finely tabulated kernel. That look-up operation is not differentiable with respect to the sampling pattern, complicating auto-differentiation routines for backpropagation (stochastic gradient descent) for sampling pattern optimization. This paper describes an efficient and accurate approach for computing approximate gradients with respect to the sampling pattern for learning k-space sampling. Various numerical experiments validate the accuracy of the proposed approximation. We also showcase the trajectories optimized for different iterative reconstruction algorithms, including smooth convex regularized reconstruction and compressed sensing-based reconstruction.