Edge-exchangeable graphs and sparsity (NIPS 2016)
Paper and Code
Feb 03, 2017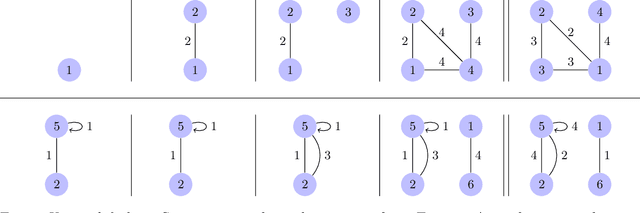
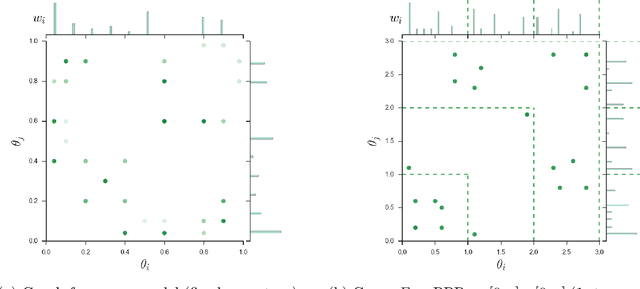
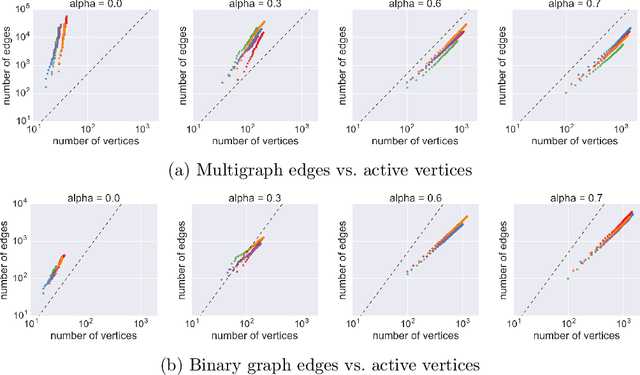
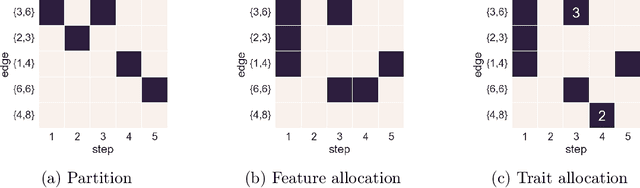
Many popular network models rely on the assumption of (vertex) exchangeability, in which the distribution of the graph is invariant to relabelings of the vertices. However, the Aldous-Hoover theorem guarantees that these graphs are dense or empty with probability one, whereas many real-world graphs are sparse. We present an alternative notion of exchangeability for random graphs, which we call edge exchangeability, in which the distribution of a graph sequence is invariant to the order of the edges. We demonstrate that edge-exchangeable models, unlike models that are traditionally vertex exchangeable, can exhibit sparsity. To do so, we outline a general framework for graph generative models; by contrast to the pioneering work of Caron and Fox (2015), models within our framework are stationary across steps of the graph sequence. In particular, our model grows the graph by instantiating more latent atoms of a single random measure as the dataset size increases, rather than adding new atoms to the measure.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge