Eccentric Regularization: Minimizing Hyperspherical Energy without explicit projection

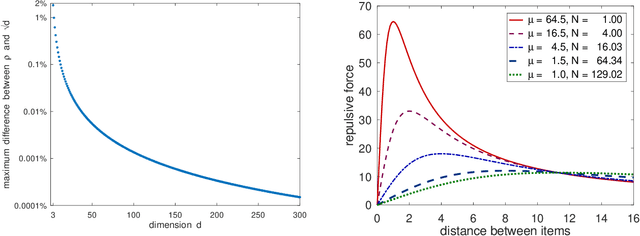
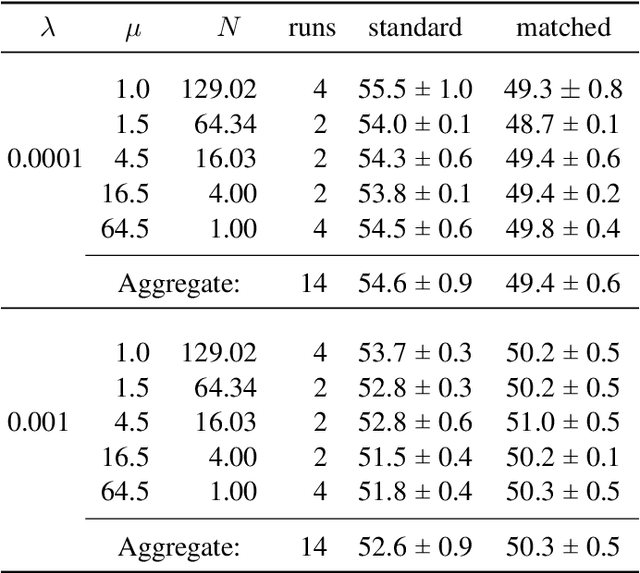
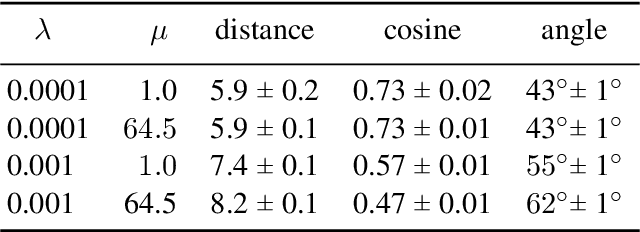
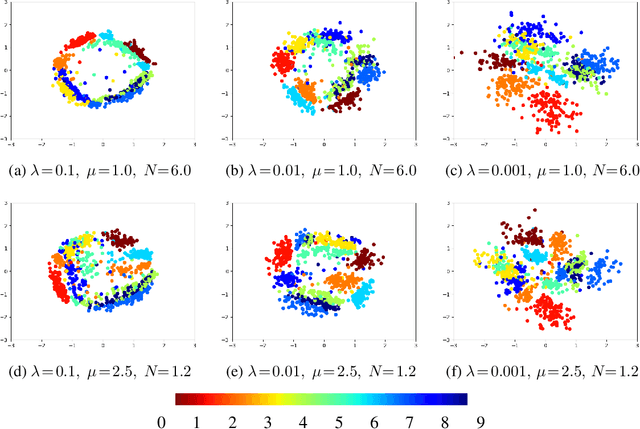
Several regularization methods have recently been introduced which force the latent activations of an autoencoder or deep neural network to conform to either a Gaussian or hyperspherical distribution, or to minimize the implicit rank of the distribution in latent space. In the present work, we introduce a novel regularizing loss function which simulates a pairwise repulsive force between items and an attractive force of each item toward the origin. We show that minimizing this loss function in isolation achieves a hyperspherical distribution. Moreover, when used as a regularizing term, the scaling factor can be adjusted to allow greater flexibility and tolerance of eccentricity, thus allowing the latent variables to be stratified according to their relative importance, while still promoting diversity. We apply this method of Eccentric Regularization to an autoencoder, and demonstrate its effectiveness in image generation, representation learning and downstream classification tasks.