e3nn: Euclidean Neural Networks
Paper and Code
Jul 18, 2022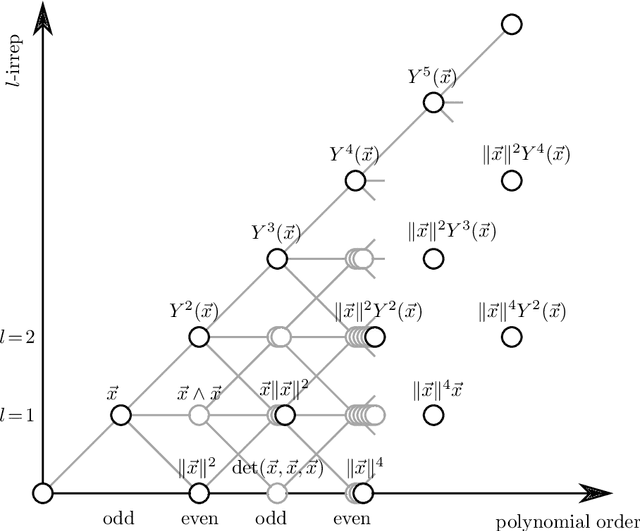
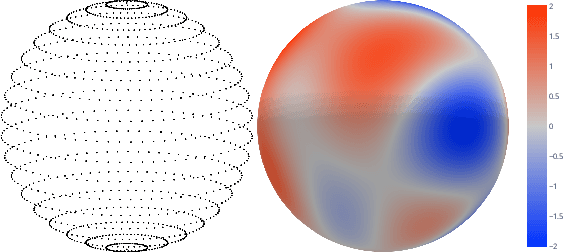
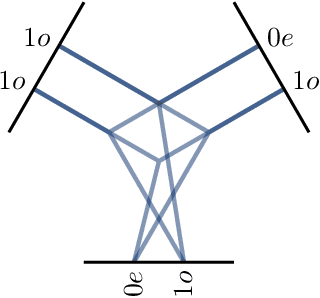
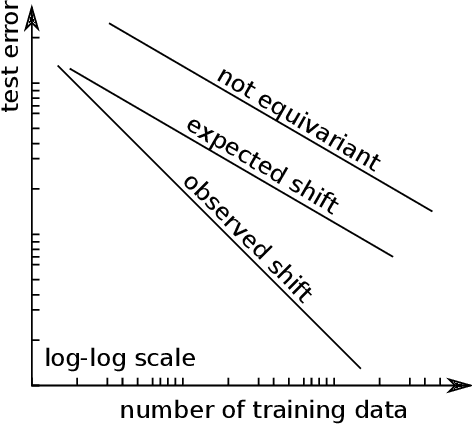
We present e3nn, a generalized framework for creating E(3) equivariant trainable functions, also known as Euclidean neural networks. e3nn naturally operates on geometry and geometric tensors that describe systems in 3D and transform predictably under a change of coordinate system. The core of e3nn are equivariant operations such as the TensorProduct class or the spherical harmonics functions that can be composed to create more complex modules such as convolutions and attention mechanisms. These core operations of e3nn can be used to efficiently articulate Tensor Field Networks, 3D Steerable CNNs, Clebsch-Gordan Networks, SE(3) Transformers and other E(3) equivariant networks.
* draft
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge