Dynamical softassign and adaptive parameter tuning for graph matching

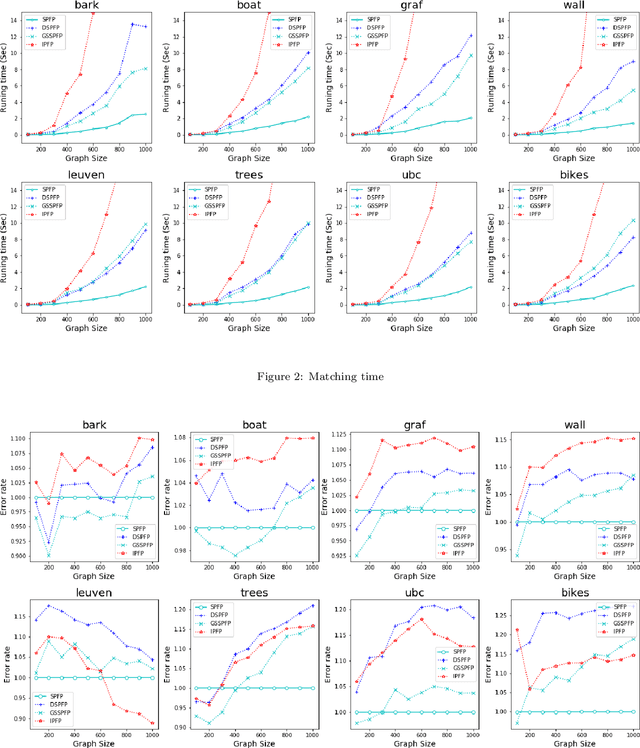
This paper studies a framework, projected fixed-point method, for graph matching. The framework contains a class of popular graph matching algorithms, including graduated assignment (GA), integer projected fixed-point method (IPFP) and doubly stochastic projected fixed-point method (DSPFP). We propose an adaptive strategy to tune the step size parameter in this framework. Such a strategy improves these algorithms in efficiency and accuracy. Further, it guarantees the convergence of the underlying algorithms. Some preliminary analysis based on distance geometry seems to support that the optimal step size parameter has a high probability of 1 when graphs are fully connected. Secondly, it is observed that a popular projection method, softassign, is sensitive to graphs' cardinality(size). We proposed a dynamical softassign algorithm that is robust to graphs' cardinality. Combining the adaptive step size and the dynamical softassign, we propose a novel graph matching algorithm: the adaptive projected fixed-point method with dynamical softassign. Various experiments demonstrate that the proposed algorithm is significantly faster than several other state-of-art algorithms with no loss of accuracy.