Dynamic Scheduling for Minimizing AoI in Resource-Constrained Multi-Source Relaying Systems with Stochastic Arrivals

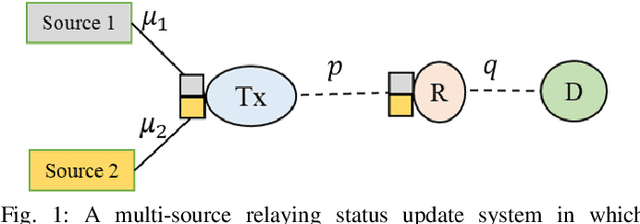
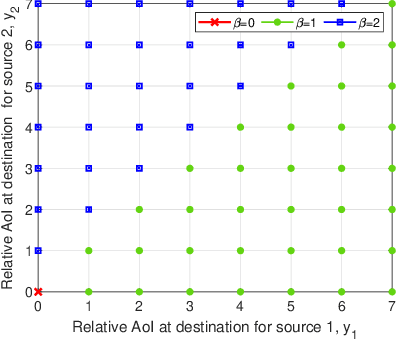
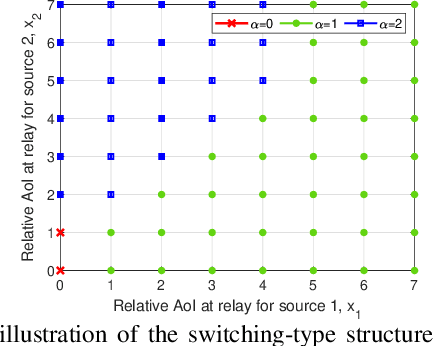
We consider a multi-source relaying system where the independent sources randomly generate status update packets which are sent to the destination with the aid of a relay through unreliable links. We develop scheduling policies to minimize the sum average age of information (AoI) subject to transmission capacity and long-run average resource constraints. We formulate a stochastic optimization problem and solve it under two different scenarios regarding the knowledge of system statistics: known environment and unknown environment. For the known environment, a constrained Markov decision process (CMDP) approach and a drift-plus-penalty method are proposed. The CMDP problem is solved by transforming it into an MDP problem using the Lagrangian relaxation method. We theoretically analyze the structure of optimal policies for the MDP problem and subsequently propose a structure-aware algorithm that returns a practical near-optimal policy. By the drift-plus-penalty method, we devise a dynamic near-optimal low-complexity policy. For the unknown environment, we develop a deep reinforcement learning policy by employing the Lyapunov optimization theory and a dueling double deep Q-network. Simulation results are provided to assess the performance of our policies and validate the theoretical results. The results show up to 91% performance improvement compared to a baseline policy.