Dynamic Sasvi: Strong Safe Screening for Norm-Regularized Least Squares
Paper and Code
Feb 08, 2021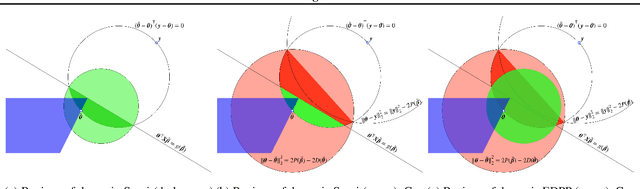
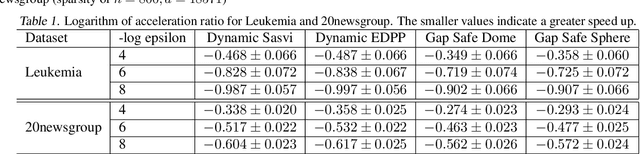
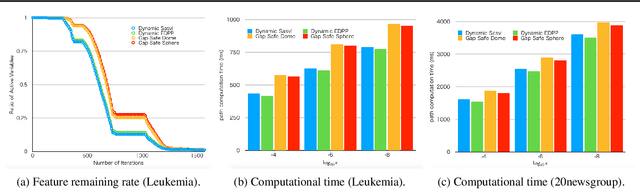
A recently introduced technique for a sparse optimization problem called "safe screening" allows us to identify irrelevant variables in the early stage of optimization. In this paper, we first propose a flexible framework for safe screening based on the Fenchel-Rockafellar duality and then derive a strong safe screening rule for norm-regularized least squares by the framework. We call the proposed screening rule for norm-regularized least squares "dynamic Sasvi" because it can be interpreted as a generalization of Sasvi. Unlike the original Sasvi, it does not require the exact solution of a more strongly regularized problem; hence, it works safely in practice. We show that our screening rule can eliminate more features and increase the speed of the solver in comparison with other screening rules both theoretically and experimentally.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge