Dynamic Regularizer with an Informative Prior

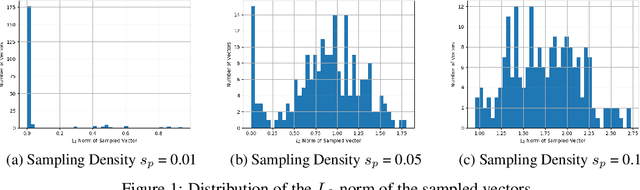
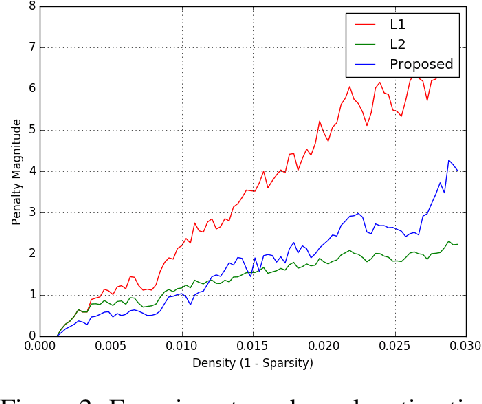
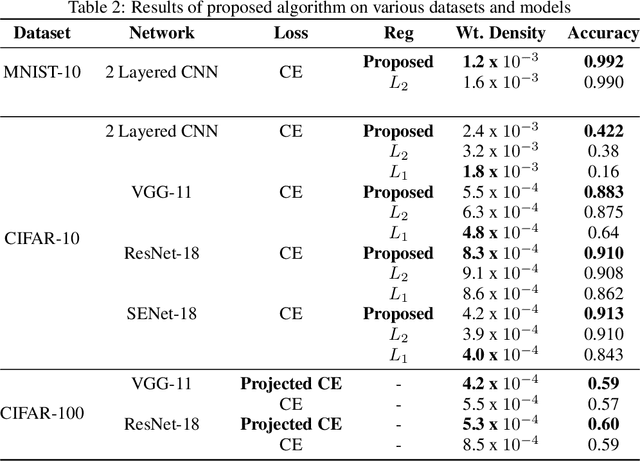
Regularization methods, specifically those which directly alter weights like $L_1$ and $L_2$, are an integral part of many learning algorithms. Both the regularizers mentioned above are formulated by assuming certain priors in the parameter space and these assumptions, in some cases, induce sparsity in the parameter space. Regularizers help in transferring beliefs one has on the dataset or the parameter space by introducing adequate terms in the loss function. Any kind of formulation represents a specific set of beliefs: $L_1$ regularization conveys that the parameter space should be sparse whereas $L_2$ regularization conveys that the parameter space should be bounded and continuous. These regularizers in turn leverage certain priors to express these inherent beliefs. A better understanding of how the prior affects the behavior of the parameters and how the priors can be updated based on the dataset can contribute greatly in improving the generalization capabilities of a function estimator. In this work, we introduce a weakly informative prior and then further extend it to an informative prior in order to formulate a regularization penalty, which shows better results in terms of inducing sparsity experimentally, when compared to regularizers based only on Gaussian and Laplacian priors. Experimentally, we verify that a regularizer based on an adapted prior improves the generalization capabilities of any network. We illustrate the performance of the proposed method on the MNIST and CIFAR-10 datasets.