Dynamic Filters in Graph Convolutional Neural Networks
Paper and Code
May 26, 2021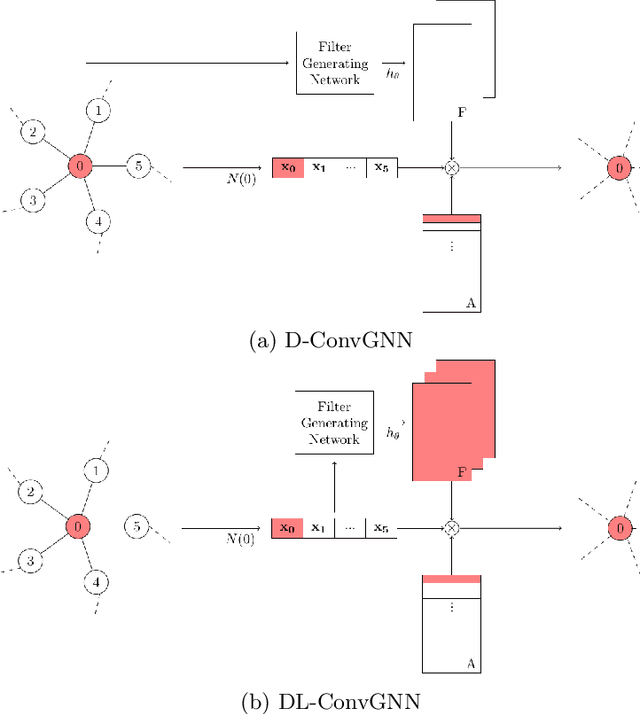
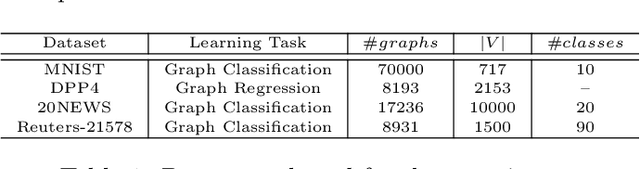
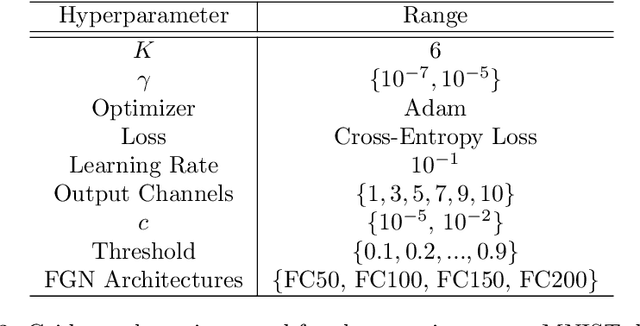
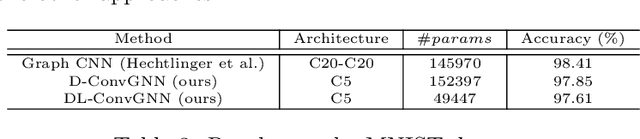
Over the last few years, we have seen increasing data generated from non-Euclidean domains, which are usually represented as graphs with complex relationships, and Graph Neural Networks (GNN) have gained a high interest because of their potential in processing graph-structured data. In particular, there is a strong interest in exploring the possibilities in performing convolution on graphs using an extension of the GNN architecture, generally referred to as Graph Convolutional Neural Networks (GCNN). Convolution on graphs has been achieved mainly in two forms: spectral and spatial convolutions. Due to the higher flexibility in exploring and exploiting the graph structure of data, recently, there is an increasing interest in investigating the possibilities that the spatial approach can offer. The idea of finding a way to adapt the network behaviour to the inputs they process to maximize the total performances has aroused much interest in the neural networks literature over the years. This paper presents a novel method to adapt the behaviour of a GCNN to the input proposing two ways to perform spatial convolution on graphs using input-based filters which are dynamically generated. Our model also investigates the problem of discovering and refining relations among nodes. The experimental assessment confirms the capabilities of the proposed approach, which achieves satisfying results using simple architectures with a low number of filters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge