DSL: Discriminative Subgraph Learning via Sparse Self-Representation
Paper and Code
Mar 24, 2019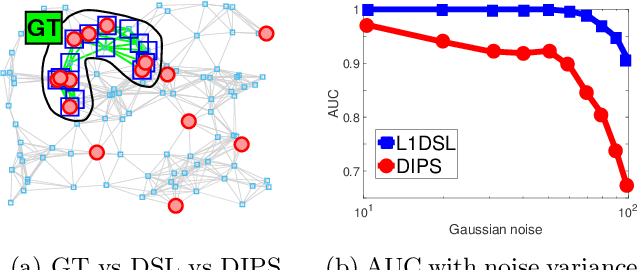
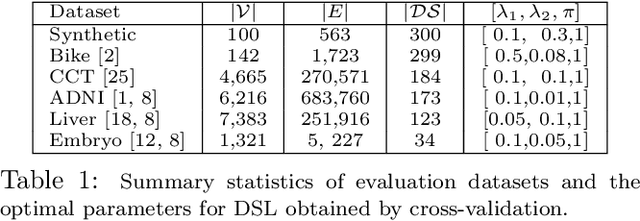

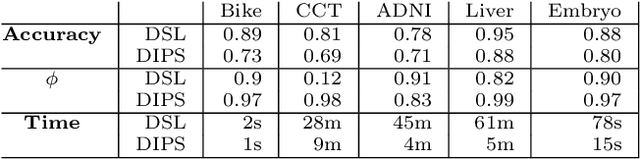
The goal in network state prediction (NSP) is to classify the global state (label) associated with features embedded in a graph. This graph structure encoding feature relationships is the key distinctive aspect of NSP compared to classical supervised learning. NSP arises in various applications: gene expression samples embedded in a protein-protein interaction (PPI) network, temporal snapshots of infrastructure or sensor networks, and fMRI coherence network samples from multiple subjects to name a few. Instances from these domains are typically ``wide'' (more features than samples), and thus, feature sub-selection is required for robust and generalizable prediction. How to best employ the network structure in order to learn succinct connected subgraphs encompassing the most discriminative features becomes a central challenge in NSP. Prior work employs connected subgraph sampling or graph smoothing within optimization frameworks, resulting in either large variance of quality or weak control over the connectivity of selected subgraphs. In this work we propose an optimization framework for discriminative subgraph learning (DSL) which simultaneously enforces (i) sparsity, (ii) connectivity and (iii) high discriminative power of the resulting subgraphs of features. Our optimization algorithm is a single-step solution for the NSP and the associated feature selection problem. It is rooted in the rich literature on maximal-margin optimization, spectral graph methods and sparse subspace self-representation. DSL simultaneously ensures solution interpretability and superior predictive power (up to 16% improvement in challenging instances compared to baselines), with execution times up to an hour for large instances.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge