Diversity and degrees of freedom in regression ensembles
Paper and Code
Mar 01, 2018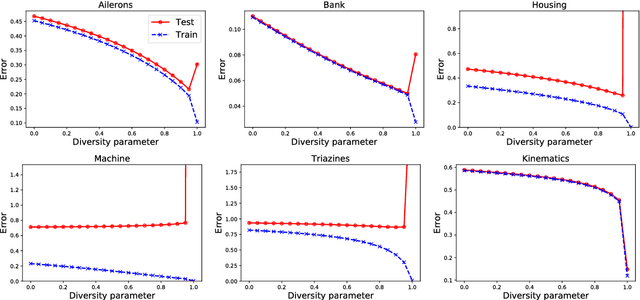
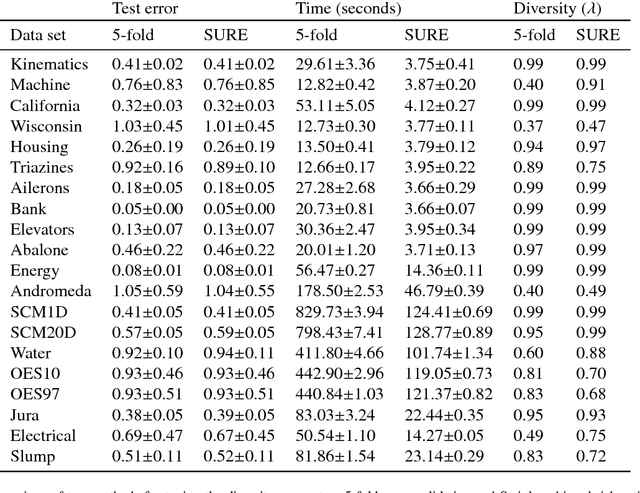
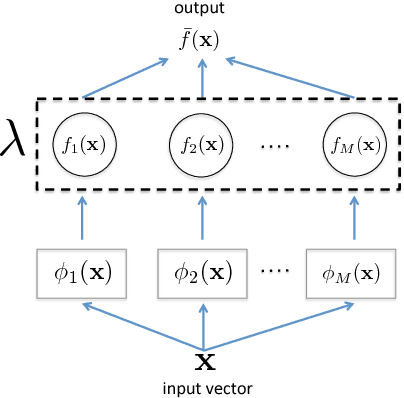
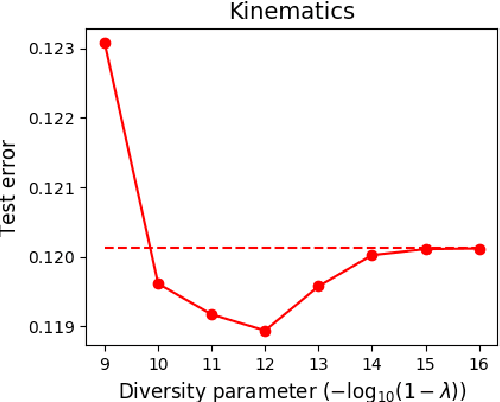
Ensemble methods are a cornerstone of modern machine learning. The performance of an ensemble depends crucially upon the level of diversity between its constituent learners. This paper establishes a connection between diversity and degrees of freedom (i.e. the capacity of the model), showing that diversity may be viewed as a form of inverse regularisation. This is achieved by focusing on a previously published algorithm Negative Correlation Learning (NCL), in which model diversity is explicitly encouraged through a diversity penalty term in the loss function. We provide an exact formula for the effective degrees of freedom in an NCL ensemble with fixed basis functions, showing that it is a continuous, convex and monotonically increasing function of the diversity parameter. We demonstrate a connection to Tikhonov regularisation and show that, with an appropriately chosen diversity parameter, an NCL ensemble can always outperform the unregularised ensemble in the presence of noise. We demonstrate the practical utility of our approach by deriving a method to efficiently tune the diversity parameter. Finally, we use a Monte-Carlo estimator to extend the connection between diversity and degrees of freedom to ensembles of deep neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge