Dithered backprop: A sparse and quantized backpropagation algorithm for more efficient deep neural network training
Paper and Code
Apr 16, 2020
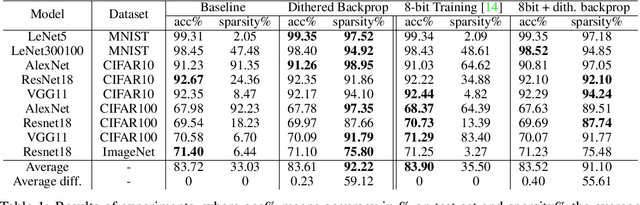
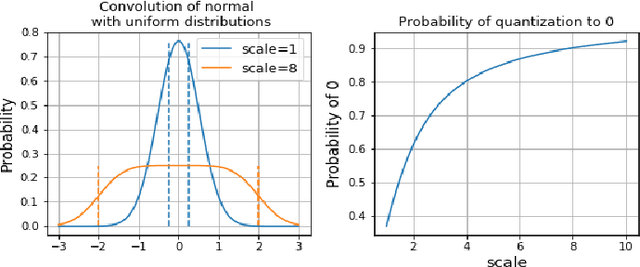
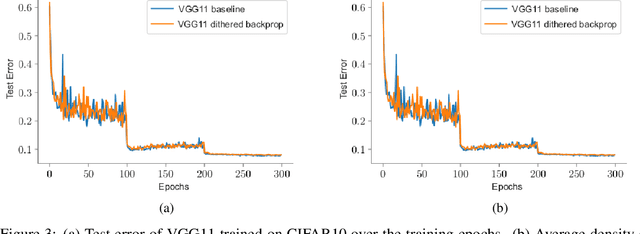
Deep Neural Networks are successful but highly computationally expensive learning systems. One of the main sources of time and energy drains is the well known backpropagation (backprop) algorithm, which roughly accounts for 2/3 of the computational complexity of training. In this work we propose a method for reducing the computational cost of backprop, which we named dithered backprop. It consists in applying a stochastic quantization scheme to intermediate results of the method. The particular quantisation scheme, called non-subtractive dither (NSD), induces sparsity which can be exploited by computing efficient sparse matrix multiplications. Experiments on popular image classification tasks show that it induces 92% sparsity on average across a wide set of models at no or negligible accuracy drop in comparison to state-of-the-art approaches, thus significantly reducing the computational complexity of the backward pass. Moreover, we show that our method is fully compatible to state-of-the-art training methods that reduce the bit-precision of training down to 8-bits, as such being able to further reduce the computational requirements. Finally we discuss and show potential benefits of applying dithered backprop in a distributed training setting, where both communication as well as compute efficiency may increase simultaneously with the number of participant nodes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge