Distribution-free conditional predictive bands using density estimators
Paper and Code
Oct 12, 2019
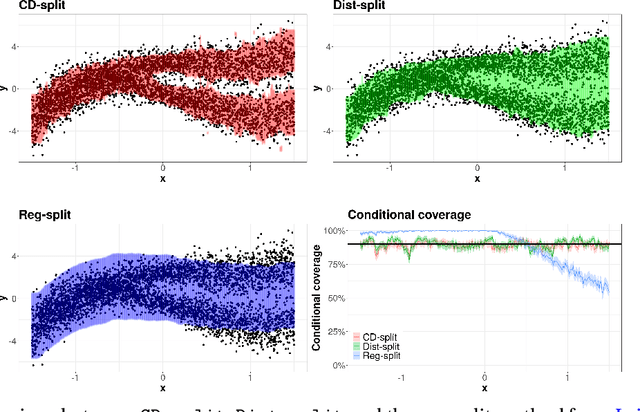
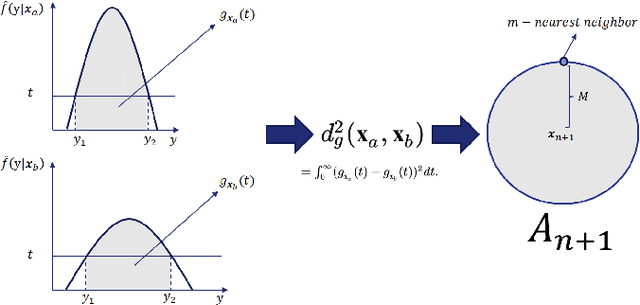
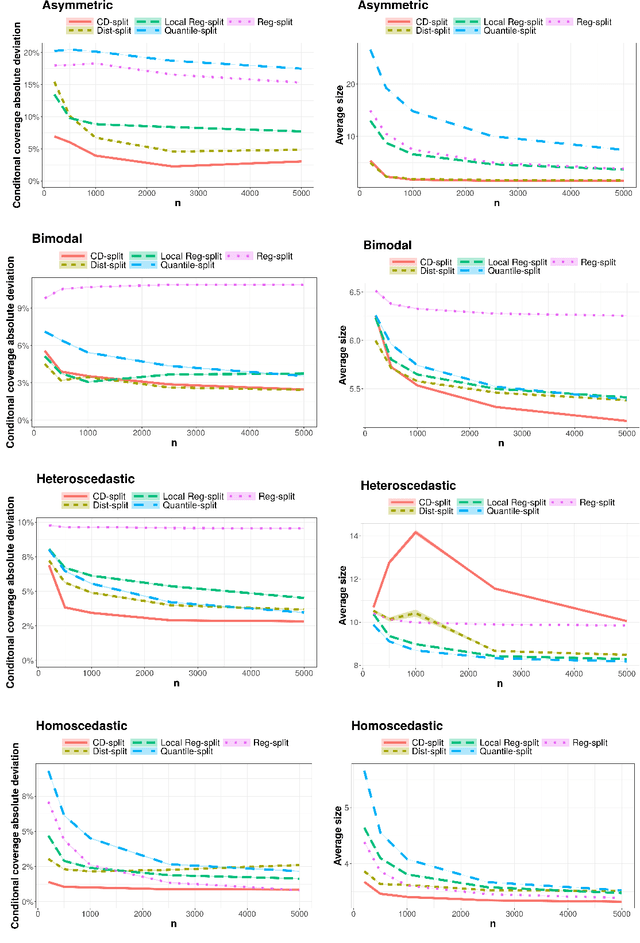
Conformal methods create prediction bands that control average coverage under no assumptions besides i.i.d. data. Besides average coverage, one might also desire to control conditional coverage, that is, coverage for every new testing point. However, without strong assumptions, conditional coverage is unachievable. Given this limitation, the literature has focused on methods with asymptotical conditional coverage. In order to obtain this property, these methods require strong conditions on the dependence between the target variable and the features. We introduce two conformal methods based on conditional density estimators that do not depend on this type of assumption to obtain asymptotic conditional coverage: Dist-split and CD-split. While Dist-split asymptotically obtains optimal intervals, which are easier to interpret than general regions, CD-split obtains optimal size regions, which are smaller than intervals. CD-split also obtains local coverage by creating a data-driven partition of the feature space that scales to high-dimensional settings and by generating prediction bands locally on the partition elements. In a wide variety of simulated scenarios, our methods have a better control of conditional coverage and have smaller length than previously proposed methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge