Distributed TD(0) with Almost No Communication
Paper and Code
May 25, 2023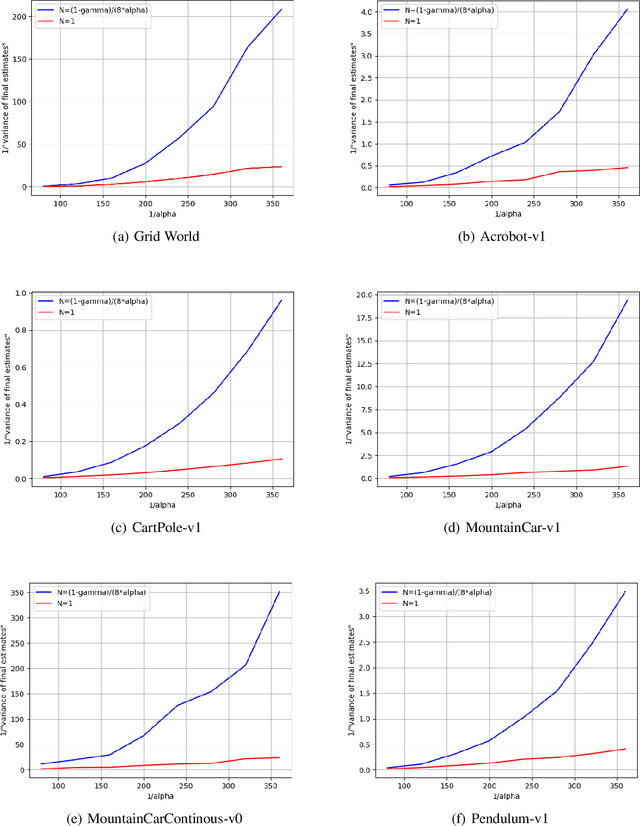
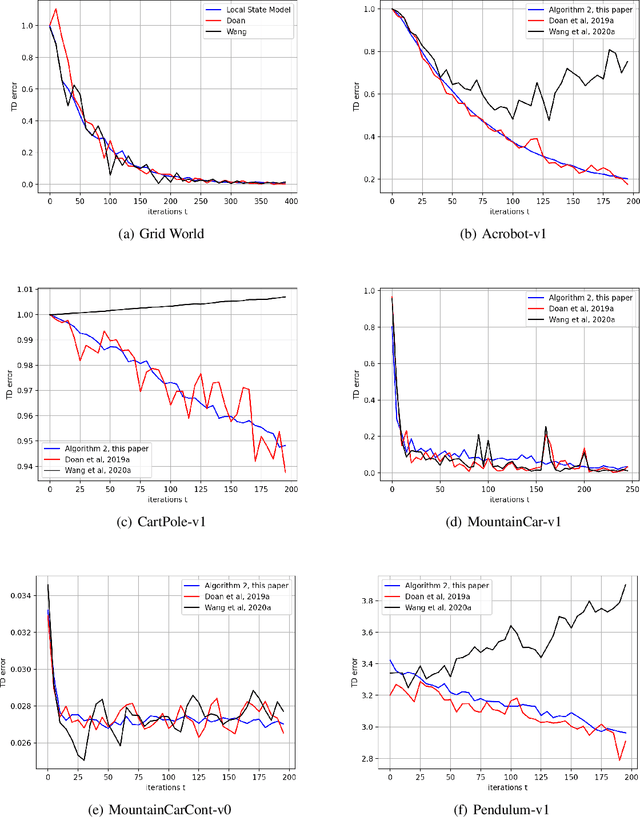
We provide a new non-asymptotic analysis of distributed temporal difference learning with linear function approximation. Our approach relies on ``one-shot averaging,'' where $N$ agents run identical local copies of the TD(0) method and average the outcomes only once at the very end. We demonstrate a version of the linear time speedup phenomenon, where the convergence time of the distributed process is a factor of $N$ faster than the convergence time of TD(0). This is the first result proving benefits from parallelism for temporal difference methods.
* This is a shortened version of arXiv:2104.07855
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge