Distributed Task Management in the Heterogeneous Fog: A Socially Concave Bandit Game

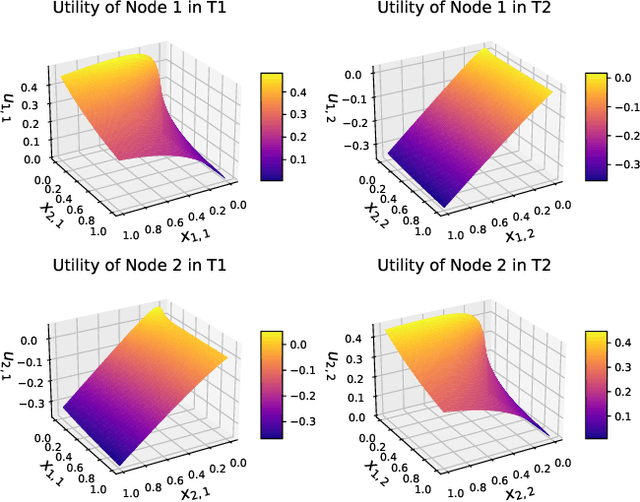
Fog computing has emerged as a potential solution to the explosive computational demand of mobile users. This potential mainly stems from the capacity of task offloading and allocation at the network edge, which reduces the delay and improves the quality of service. Despite the significant potential, optimizing the performance of a fog network is often challenging. In the fog architecture, the computing nodes are heterogeneous smart devices with distinct abilities and capacities, thereby, preferences. Besides, in an ultra-dense fog network with random task arrival, centralized control results in excessive overhead, and therefore, it is not feasible. We study a distributed task allocation problem in a heterogeneous fog computing network under uncertainty. We formulate the problem as a social-concave game, where the players attempt to minimize their regret on the path to Nash equilibrium. To solve the formulated problem, we develop two no-regret decision-making strategies. One strategy, namely bandit gradient ascent with momentum, is an online convex optimization algorithm with bandit feedback. The other strategy, Lipschitz Bandit with Initialization, is an EXP3 multi-armed bandit algorithm. We establish a regret bound for both strategies and analyze their convergence characteristics. Moreover, we compare the proposed strategies with a centralized allocation strategy named Learning with Linear Rewards. Theoretical and numerical analysis shows the superior performance of the proposed strategies for efficient task allocation compared to the state-of-the-art methods.