Distributed linear regression by averaging

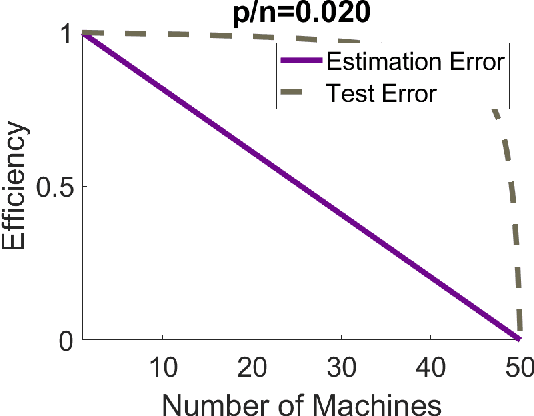
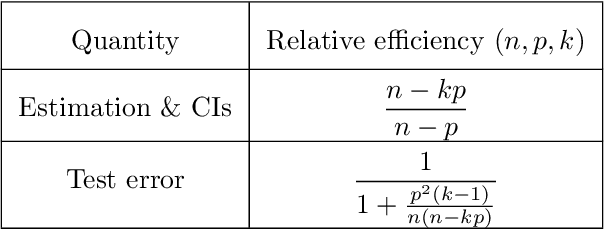
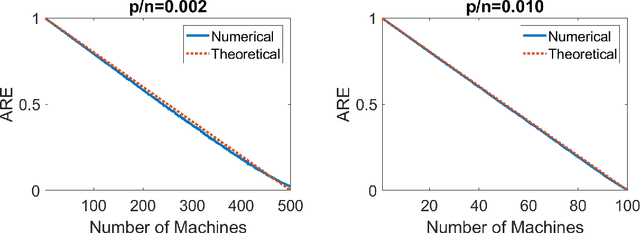
Modern massive datasets pose an enormous computational burden to practitioners. Distributed computation has emerged as a universal approach to ease the burden: Datasets are partitioned over machines, which compute locally, and communicate short messages. Distributed data also arises due to privacy reasons, such as in medicine. It is important to study how to do statistical inference and machine learning in a distributed setting. In this paper, we study one-step parameter averaging in statistical linear models under data parallelism. We do linear regression on each machine, and take a weighted average of the parameters. How much do we lose compared to doing linear regression on the full data? Here we study the performance loss in estimation error, test error, and confidence interval length in high dimensions, where the number of parameters is comparable to the training data size. We discover several key phenomena. First, averaging is not optimal, and we find the exact performance loss. Our results are simple to use in practice. Second, different problems are affected differently by the distributed framework. Estimation error and confidence interval length increases a lot, while prediction error increases much less. These results match simulations and a data analysis example. We rely on recent results from random matrix theory, where we develop a new calculus of deterministic equivalents as a tool of broader interest.