Distributed Deep Learning with Event-Triggered Communication
Paper and Code
Sep 08, 2019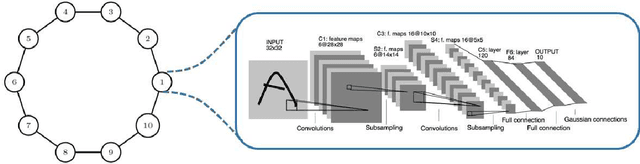
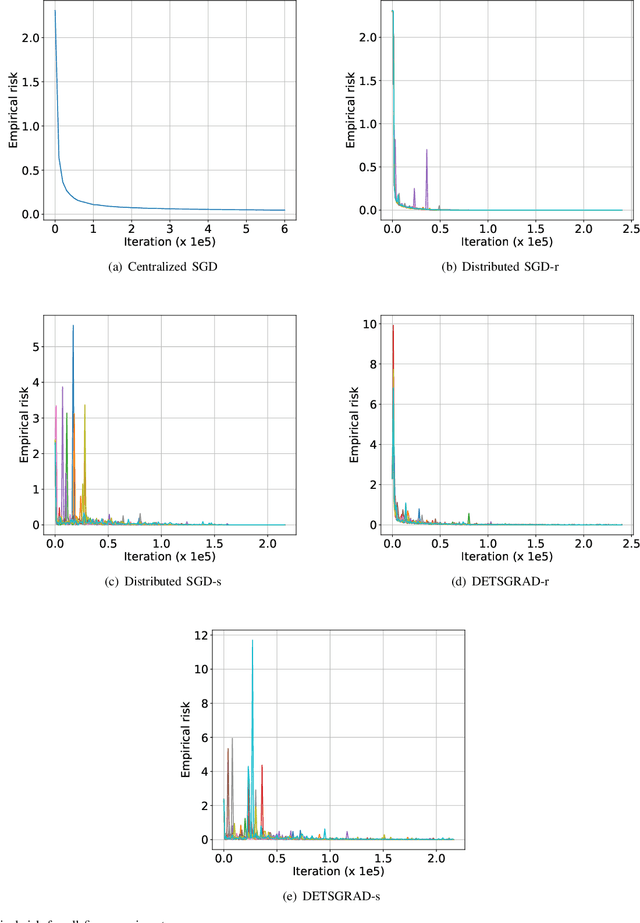
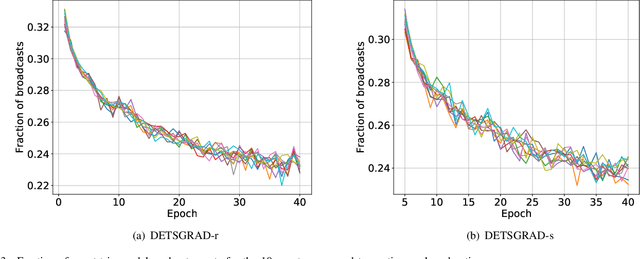
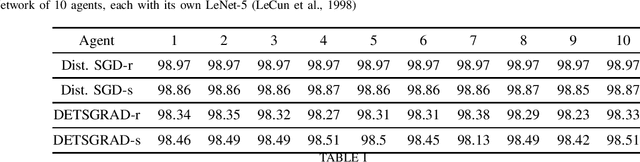
We develop a Distributed Event-Triggered Stochastic GRAdient Descent (DETSGRAD) algorithm for solving non-convex optimization problems typically encountered in distributed deep learning. We propose a novel communication triggering mechanism that would allow the networked agents to update their model parameters aperiodically and provide sufficient conditions on the algorithm step-sizes that guarantee the asymptotic mean-square convergence. The algorithm is applied to a distributed supervised-learning problem, in which a set of networked agents collaboratively train their individual neural networks to recognize handwritten digits in images, while aperiodically sharing the model parameters with their one-hop neighbors. Results indicate that all agents report similar performance that is also comparable to the performance of a centrally trained neural network, while the event-triggered communication provides significant reduction in inter-agent communication. Results also show that the proposed algorithm allows the individual agents to recognize the digits even though the training data corresponding to all the digits are not locally available to each agent.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge