Distributed Bandits: Probabilistic Communication on $d$-regular Graphs
Paper and Code
Nov 16, 2020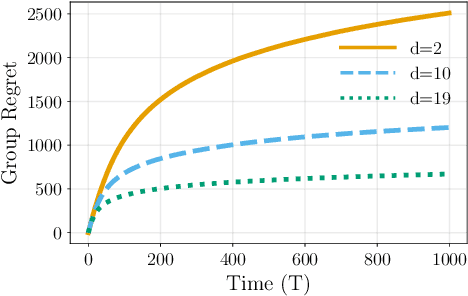
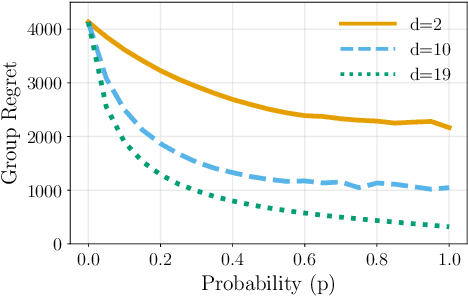
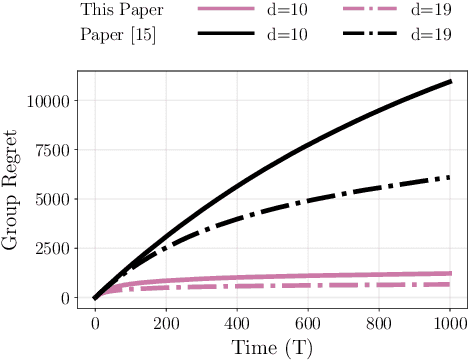
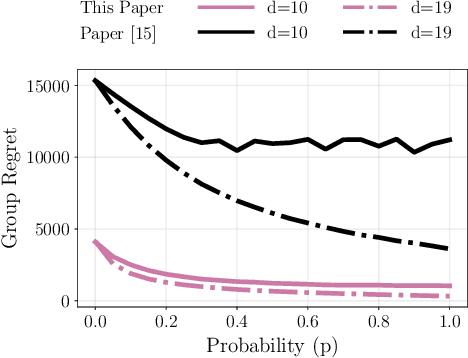
We study the decentralized multi-agent multi-armed bandit problem for agents that communicate with probability over a network defined by a $d$-regular graph. Every edge in the graph has probabilistic weight $p$ to account for the ($1\!-\!p$) probability of a communication link failure. At each time step, each agent chooses an arm and receives a numerical reward associated with the chosen arm. After each choice, each agent observes the last obtained reward of each of its neighbors with probability $p$. We propose a new Upper Confidence Bound (UCB) based algorithm and analyze how agent-based strategies contribute to minimizing group regret in this probabilistic communication setting. We provide theoretical guarantees that our algorithm outperforms state-of-the-art algorithms. We illustrate our results and validate the theoretical claims using numerical simulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge