Distributed area coverage control with imprecise robot localization: Simulation and experimental studies
Paper and Code
Dec 14, 2016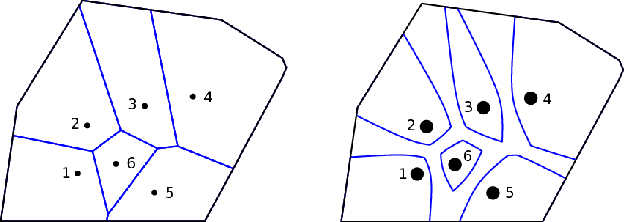
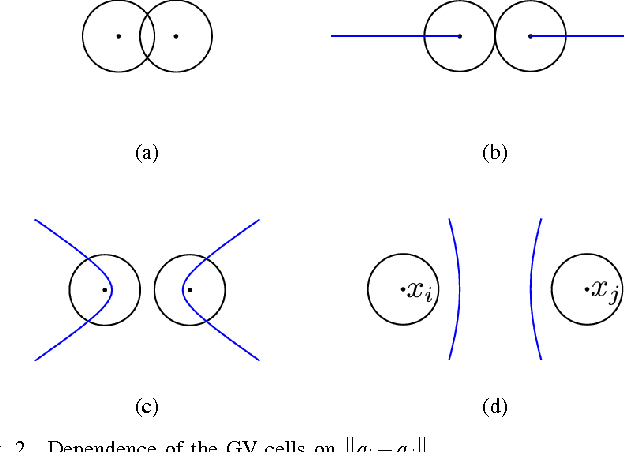
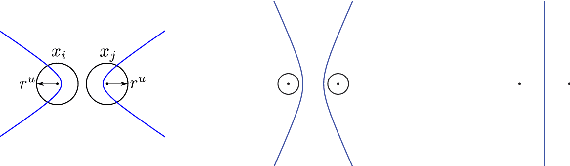
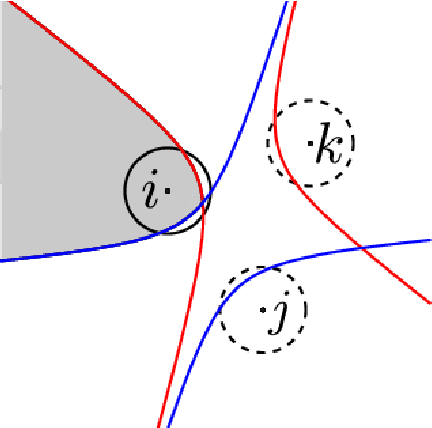
This article examines the area coverage problem for a network of mobile robots with imprecise agents' localization. Each robot has uniform radial sensing ability, governed by first order kinodynamics. The convex-space is partitioned based on the Guaranteed Voronoi (GV) principle and each robot's area of responsibility corresponds to its GV-cell, bounded by hyperbolic arcs. The proposed control law is distributed, demanding the positioning information about its GV-Delaunay neighbors. Simulation and experimental studies are offered to highlight the efficiency of the proposed control law.
* 12 pages, 28 figures, submitted to IEEE Transactions on Automatic
Control in 14 December 2016
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge