Disentangling Latent Space for VAE by Label Relevant/Irrelevant Dimensions
Paper and Code
Jan 04, 2019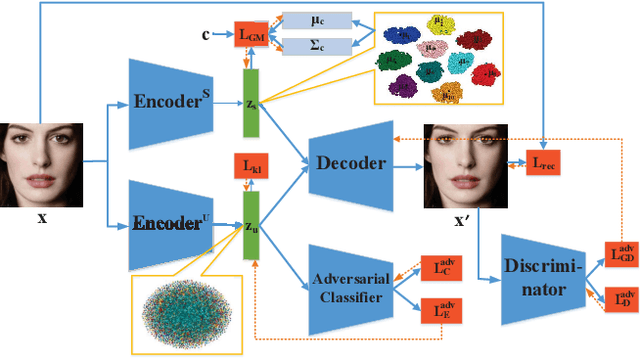
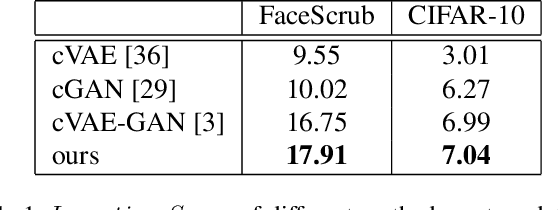
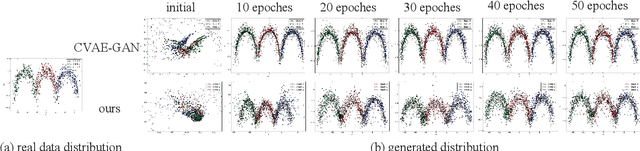
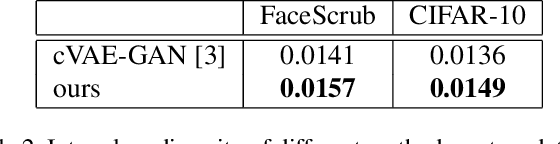
VAE requires the standard Gaussian distribution as a prior in the latent space. Since all codes tend to follow the same prior, it often suffers the so-called "posterior collapse". To avoid this, this paper introduces the class specific distribution for the latent code. But different from CVAE, we present a method for disentangling the latent space into the label relevant and irrelevant dimensions, $\bm{\mathrm{z}}_s$ and $\bm{\mathrm{z}}_u$, for a single input. We apply two separated encoders to map the input into $\bm{\mathrm{z}}_s$ and $\bm{\mathrm{z}}_u$ respectively, and then give the concatenated code to the decoder to reconstruct the input. The label irrelevant code $\bm{\mathrm{z}}_u$ represent the common characteristics of all inputs, hence they are constrained by the standard Gaussian, and their encoder is trained in amortized variational inference way, like VAE. While $\bm{\mathrm{z}}_s$ is assumed to follow the Gaussian mixture distribution in which each component corresponds to a particular class. The parameters for the Gaussian components in $\bm{\mathrm{z}}_s$ encoder are optimized by the label supervision in a global stochastic way. In theory, we show that our method is actually equivalent to adding a KL divergence term on the joint distribution of $\bm{\mathrm{z}}_s$ and the class label $c$, and it can directly increase the mutual information between $\bm{\mathrm{z}}_s$ and the label $c$. Our model can also be extended to GAN by adding a discriminator in the pixel domain so that it produces high quality and diverse images.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge