Discovering Valuable Items from Massive Data
Paper and Code
Jun 02, 2015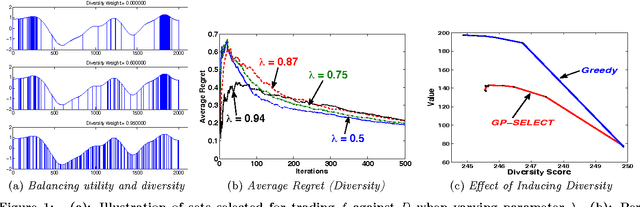
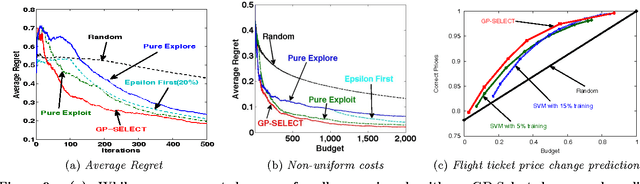
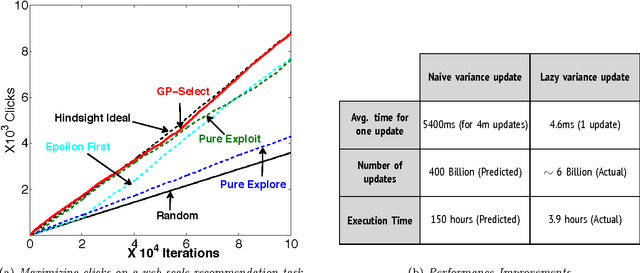
Suppose there is a large collection of items, each with an associated cost and an inherent utility that is revealed only once we commit to selecting it. Given a budget on the cumulative cost of the selected items, how can we pick a subset of maximal value? This task generalizes several important problems such as multi-arm bandits, active search and the knapsack problem. We present an algorithm, GP-Select, which utilizes prior knowledge about similarity be- tween items, expressed as a kernel function. GP-Select uses Gaussian process prediction to balance exploration (estimating the unknown value of items) and exploitation (selecting items of high value). We extend GP-Select to be able to discover sets that simultaneously have high utility and are diverse. Our preference for diversity can be specified as an arbitrary monotone submodular function that quantifies the diminishing returns obtained when selecting similar items. Furthermore, we exploit the structure of the model updates to achieve an order of magnitude (up to 40X) speedup in our experiments without resorting to approximations. We provide strong guarantees on the performance of GP-Select and apply it to three real-world case studies of industrial relevance: (1) Refreshing a repository of prices in a Global Distribution System for the travel industry, (2) Identifying diverse, binding-affine peptides in a vaccine de- sign task and (3) Maximizing clicks in a web-scale recommender system by recommending items to users.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge