Dimension Reduction Approach for Interpretability of Sequence to Sequence Recurrent Neural Networks
Paper and Code
May 29, 2019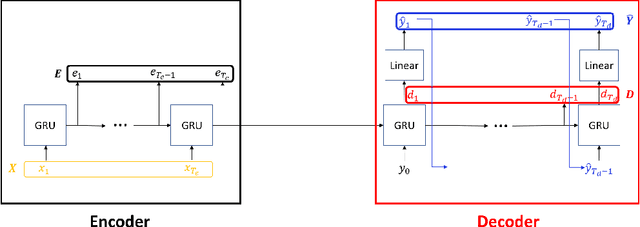
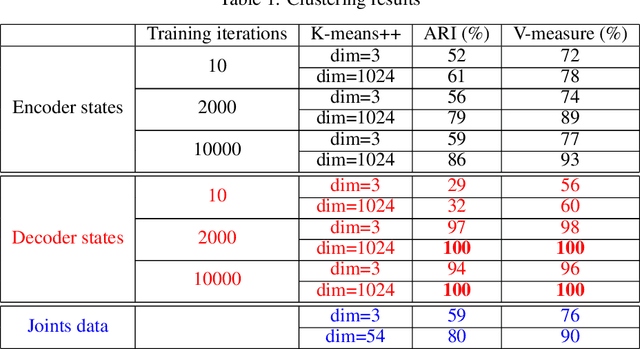
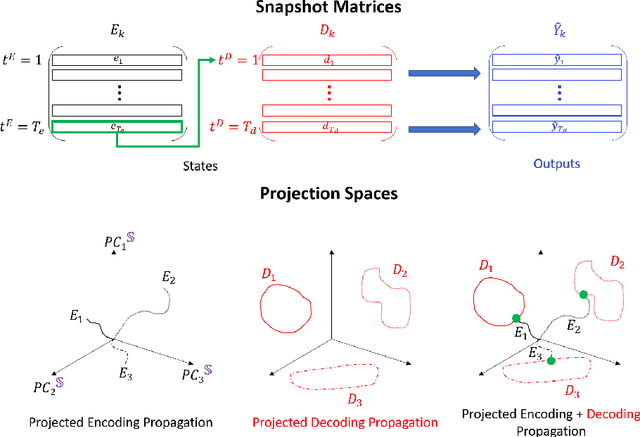
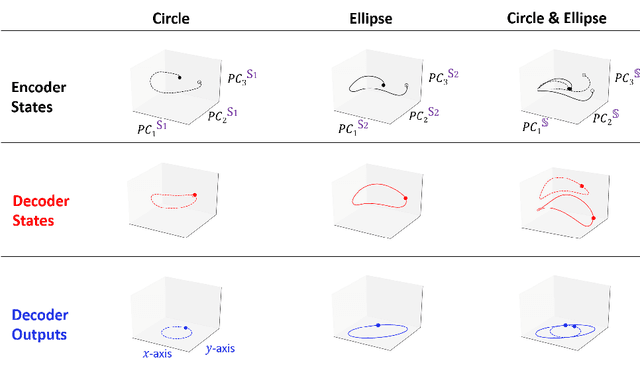
Encoder-decoder recurrent neural network models (Seq2Seq) have achieved great success in ubiquitous areas of computation and applications. It was shown to be successful in modeling data with both temporal and spatial dependencies for translation or prediction tasks. In this study, we propose a dimension reduction approach to visualize and interpret the representation of the data by these models. We propose to view the hidden states of the encoder and the decoder as spatio-temporal snapshots of network dynamics and to apply proper orthogonal decomposition to their concatenation to compute a low-dimensional embedding for hidden state dynamics. Projection of the decoder states onto such interpretable embedding space shows that Seq2Seq training to predict sequences using gradient-descent back propagation effectively performs dimension reduction consisting of only a small percentage of dimensions of the network's hidden units. Furthermore, sequences are being clustered into well separable clusters in the low dimensional space each of which corresponds to a different type of dynamics. The projection methodology also clarifies the roles of the encoder and the decoder components of the network. We show that the projection of encoder hidden states onto the low dimensional space provides an initializing trajectory directing the sequence to the cluster which corresponds to that particular type of distinct dynamics and the projection of the decoder hidden states constitutes the embedded cluster attractor. Inspection of the low dimensional space and the projections onto it during training shows that the estimation of clusters separability in the embedding can be utilized to estimate the optimality of model training. We test and demonstrate our proposed interpretability methodology on synthetic examples (dynamics on a circle and an ellipse) and on 3D human body movement data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge