Differentially Private Federated Learning via Inexact ADMM with Multiple Local Updates
Paper and Code
Feb 18, 2022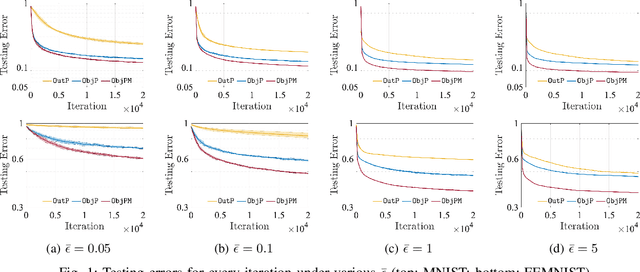
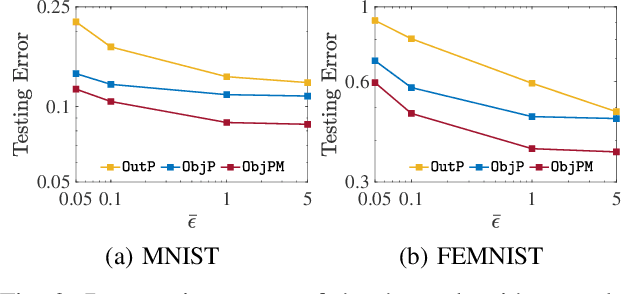
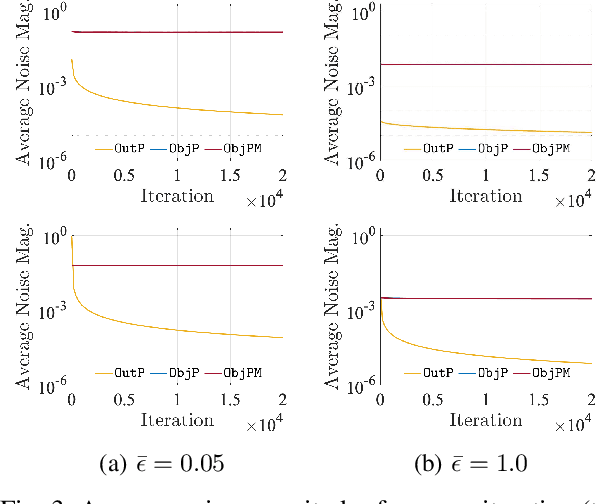
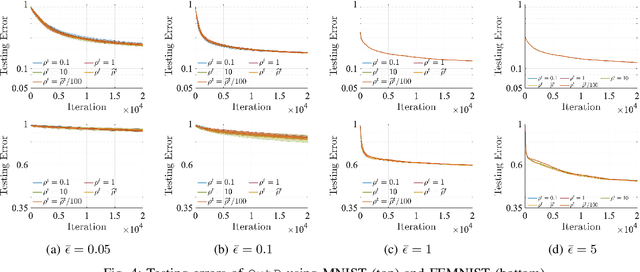
Differential privacy (DP) techniques can be applied to the federated learning model to statistically guarantee data privacy against inference attacks to communication among the learning agents. While ensuring strong data privacy, however, the DP techniques hinder achieving a greater learning performance. In this paper we develop a DP inexact alternating direction method of multipliers algorithm with multiple local updates for federated learning, where a sequence of convex subproblems is solved with the objective perturbation by random noises generated from a Laplace distribution. We show that our algorithm provides $\bar{\epsilon}$-DP for every iteration, where $\bar{\epsilon}$ is a privacy budget controlled by the user. We also present convergence analyses of the proposed algorithm. Using MNIST and FEMNIST datasets for the image classification, we demonstrate that our algorithm reduces the testing error by at most $31\%$ compared with the existing DP algorithm, while achieving the same level of data privacy. The numerical experiment also shows that our algorithm converges faster than the existing algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge