Differentially Private Distributed Mismatch Tracking Algorithm for Constraint-Coupled Resource Allocation Problems
Paper and Code
Apr 15, 2022
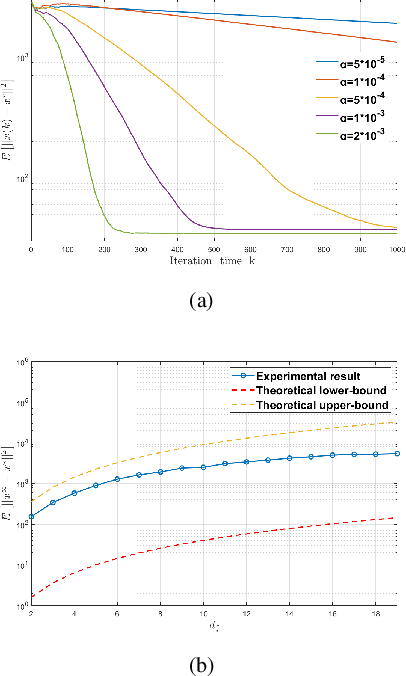
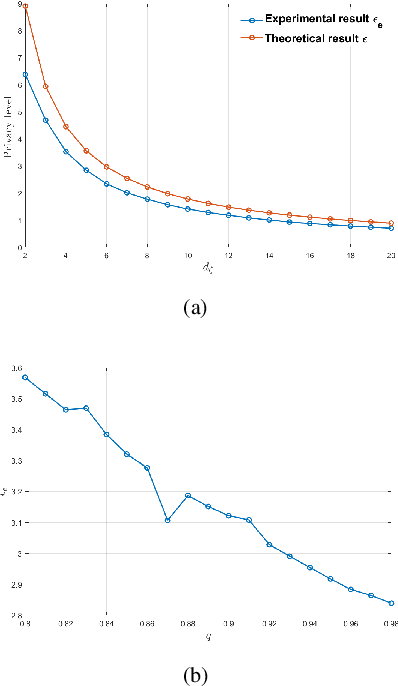
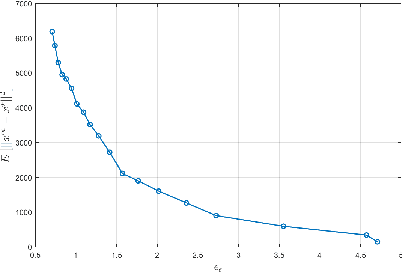
This paper considers privacy-concerned distributed constraint-coupled resource allocation problems over an undirected network, where each agent holds a private cost function and obtains the solution via only local communication. With privacy concerns, we mask the exchanged information with independent Laplace noise against a potential attacker with potential access to all network communications. We propose a differentially private distributed mismatch tracking algorithm (diff-DMAC) to achieve cost-optimal distribution of resources while preserving privacy. Adopting constant stepsizes, the linear convergence property of diff-DMAC in mean square is established under the standard assumptions of Lipschitz gradients and strong convexity. Moreover, it is theoretically proven that the proposed algorithm is {\epsilon}-differentially private.And we also show the trade-off between convergence accuracy and privacy level. Finally, a numerical example is provided for verification.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge