Differentially Private Covariance Revisited
Paper and Code
May 31, 2022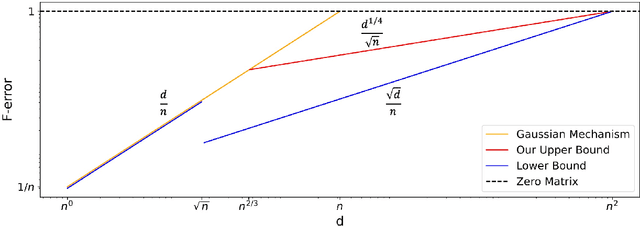
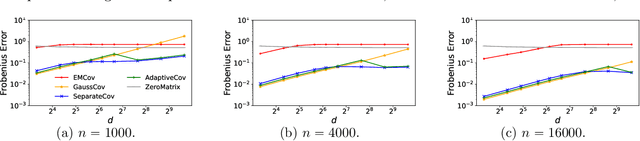
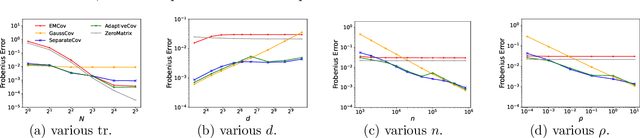
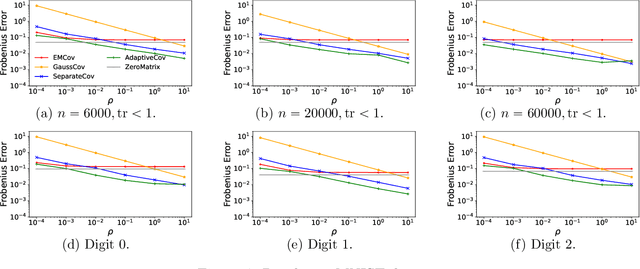
In this paper, we present three new error bounds, in terms of the Frobenius norm, for covariance estimation under differential privacy: (1) a worst-case bound of $\tilde{O}(d^{1/4}/\sqrt{n})$, which improves the standard Gaussian mechanism $\tilde{O}(d/n)$ for the regime $d>\widetilde{\Omega}(n^{2/3})$; (2) a trace-sensitive bound that improves the state of the art by a $\sqrt{d}$-factor, and (3) a tail-sensitive bound that gives a more instance-specific result. The corresponding algorithms are also simple and efficient. Experimental results show that they offer significant improvements over prior work.
View paper on
 OpenReview
OpenReview
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge