Differentially Private Bayesian Inference for Generalized Linear Models

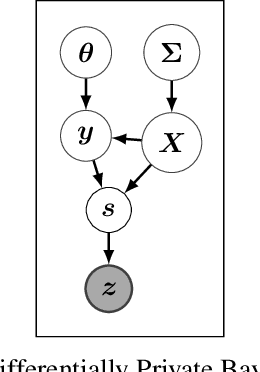
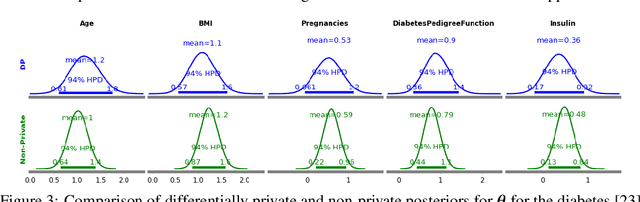
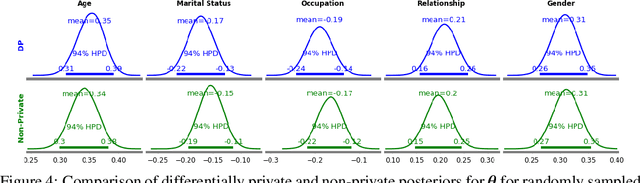
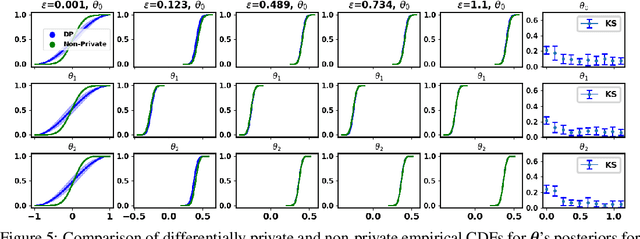
The framework of differential privacy (DP) upper bounds the information disclosure risk involved in using sensitive datasets for statistical analysis. A DP mechanism typically operates by adding carefully calibrated noise to the data release procedure. Generalized linear models (GLMs) are among the most widely used arms in data analyst's repertoire. In this work, with logistic and Poisson regression as running examples, we propose a generic noise-aware Bayesian framework to quantify the parameter uncertainty for a GLM at hand, given noisy sufficient statistics. We perform a tight privacy analysis and experimentally demonstrate that the posteriors obtained from our model, while adhering to strong privacy guarantees, are similar to the non-private posteriors.