Differentiable Rendering with Perturbed Optimizers

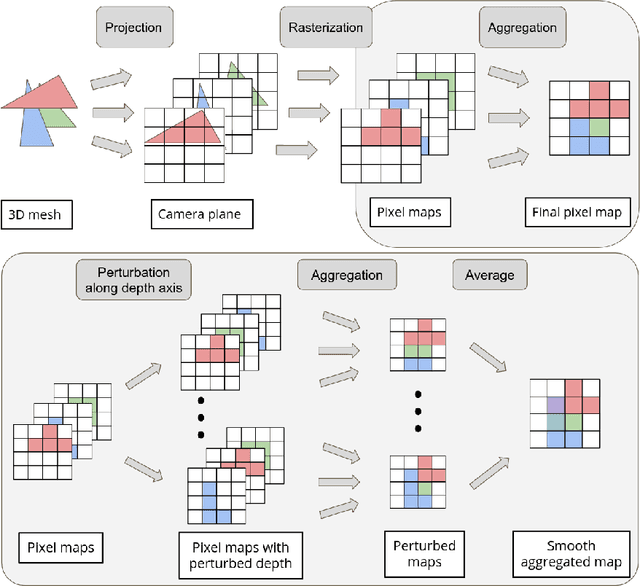
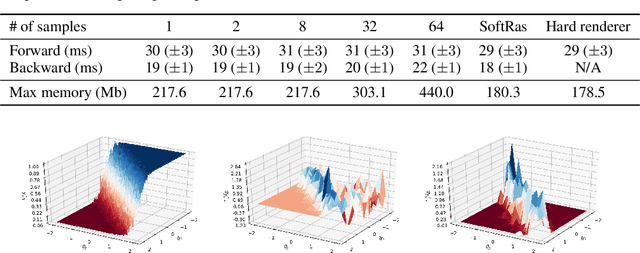
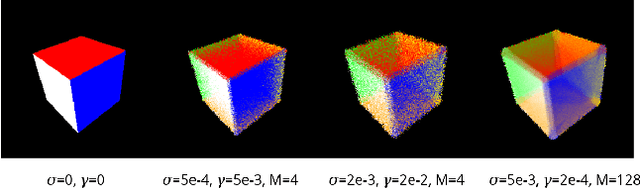
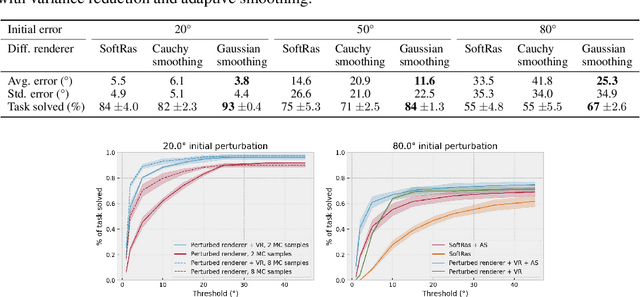
Reasoning about 3D scenes from their 2D image projections is one of the core problems in computer vision. Solutions to this inverse and ill-posed problem typically involve a search for models that best explain observed image data. Notably, images depend both on the properties of observed scenes and on the process of image formation. Hence, if optimization techniques should be used to explain images, it is crucial to design differentiable functions for the projection of 3D scenes into images, also known as differentiable rendering. Previous approaches to differentiable rendering typically replace non-differentiable operations by smooth approximations, impacting the subsequent 3D estimation. In this paper, we take a more general approach and study differentiable renderers through the prism of randomized optimization and the related notion of perturbed optimizers. In particular, our work highlights the link between some well-known differentiable renderer formulations and randomly smoothed optimizers, and introduces differentiable perturbed renderers. We also propose a variance reduction mechanism to alleviate the computational burden inherent to perturbed optimizers and introduce an adaptive scheme to automatically adjust the smoothing parameters of the rendering process. We apply our method to 3D scene reconstruction and demonstrate its advantages on the tasks of 6D pose estimation and 3D mesh reconstruction. By providing informative gradients that can be used as a strong supervisory signal, we demonstrate the benefits of perturbed renderers to obtain more accurate solutions when compared to the state-of-the-art alternatives using smooth gradient approximations.