Differentiable Expected Hypervolume Improvement for Parallel Multi-Objective Bayesian Optimization

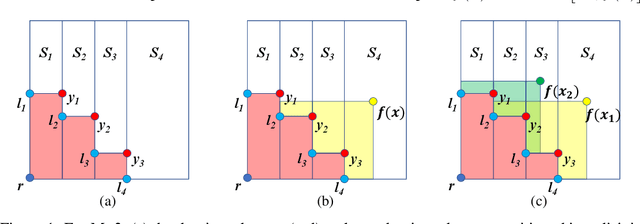
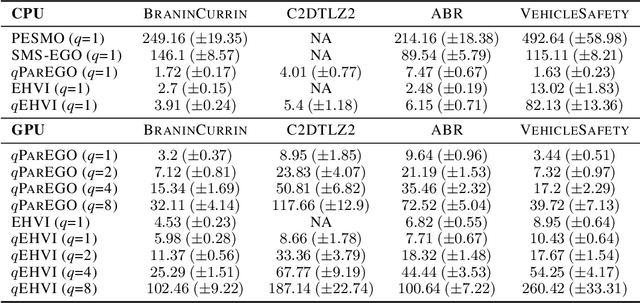
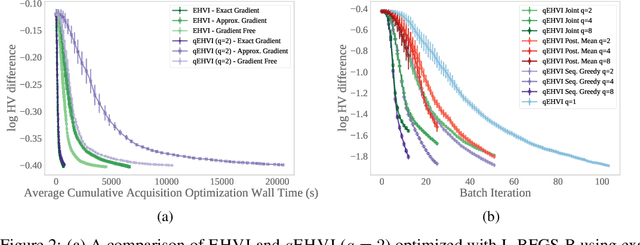
In many real-world scenarios, decision makers seek to efficiently optimize multiple competing objectives in a sample-efficient fashion. Multi-objective Bayesian optimization (BO) is a common approach, but many existing acquisition functions do not have known analytic gradients and suffer from high computational overhead. We leverage recent advances in programming models and hardware acceleration for multi-objective BO using Expected Hypervolume Improvement (EHVI)---an algorithm notorious for its high computational complexity. We derive a novel formulation of $q$-Expected Hypervolume Improvement ($q$EHVI), an acquisition function that extends EHVI to the parallel, constrained evaluation setting. $q$EHVI is an exact computation of the joint EHVI of $q$ new candidate points (up to Monte-Carlo (MC) integration error). Whereas previous EHVI formulations rely on gradient-free acquisition optimization or approximated gradients, we compute exact gradients of the MC estimator via auto-differentiation, thereby enabling efficient and effective optimization using first-order and quasi-second-order methods. Lastly, our empirical evaluation demonstrates that $q$EHVI is computationally tractable in many practical scenarios and outperforms state-of-the-art multi-objective BO algorithms at a fraction of their wall time.