Differentiable Divergences Between Time Series

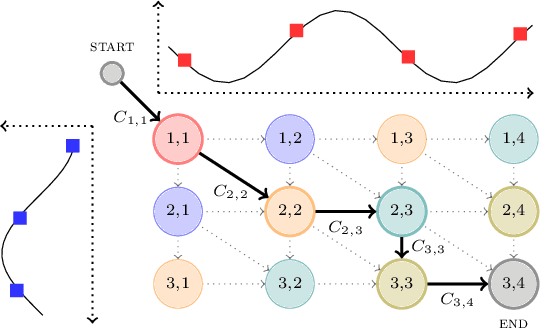
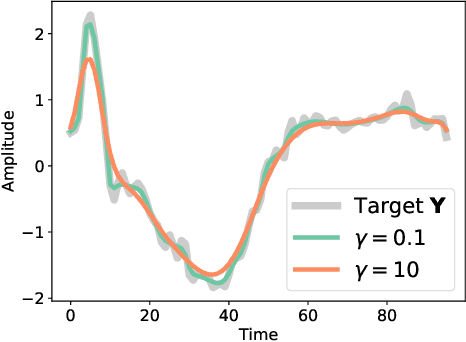
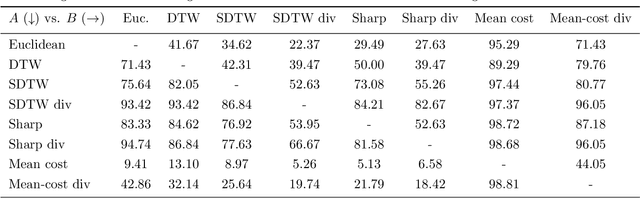
Computing the discrepancy between time series of variable sizes is notoriously challenging. While dynamic time warping (DTW) is popularly used for this purpose, it is not differentiable everywhere and is known to lead to bad local optima when used as a "loss". Soft-DTW addresses these issues, but it is not a positive definite divergence: due to the bias introduced by entropic regularization, it can be negative and it is not minimized when the time series are equal. We propose in this paper a new divergence, dubbed soft-DTW divergence, which aims to correct these issues. We study its properties; in particular, under conditions on the ground cost, we show that it is non-negative and minimized when the time series are equal. We also propose a new "sharp" variant by further removing entropic bias. We showcase our divergences on time series averaging and demonstrate significant accuracy improvements compared to both DTW and soft-DTW on 84 time series classification datasets.