Differentiable Deep Clustering with Cluster Size Constraints
Paper and Code
Oct 20, 2019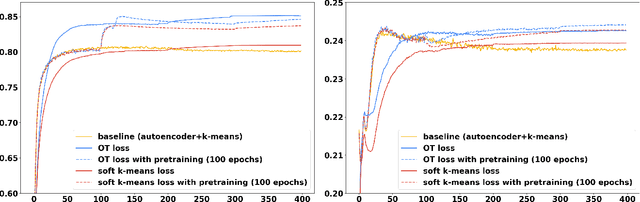
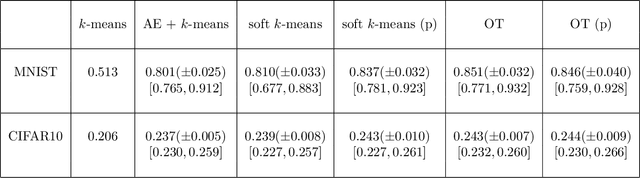
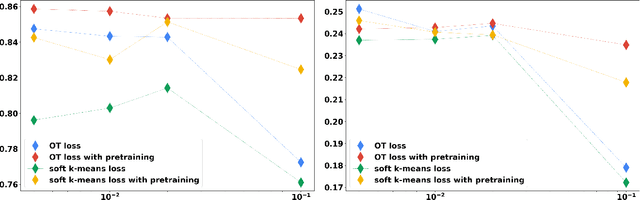
Clustering is a fundamental unsupervised learning approach. Many clustering algorithms -- such as $k$-means -- rely on the euclidean distance as a similarity measure, which is often not the most relevant metric for high dimensional data such as images. Learning a lower-dimensional embedding that can better reflect the geometry of the dataset is therefore instrumental for performance. We propose a new approach for this task where the embedding is performed by a differentiable model such as a deep neural network. By rewriting the $k$-means clustering algorithm as an optimal transport task, and adding an entropic regularization, we derive a fully differentiable loss function that can be minimized with respect to both the embedding parameters and the cluster parameters via stochastic gradient descent. We show that this new formulation generalizes a recently proposed state-of-the-art method based on soft-$k$-means by adding constraints on the cluster sizes. Empirical evaluations on image classification benchmarks suggest that compared to state-of-the-art methods, our optimal transport-based approach provide better unsupervised accuracy and does not require a pre-training phase.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge