Deviance Matrix Factorization
Paper and Code
Oct 12, 2021
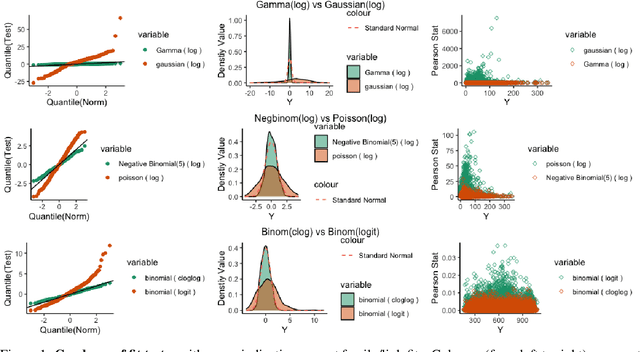
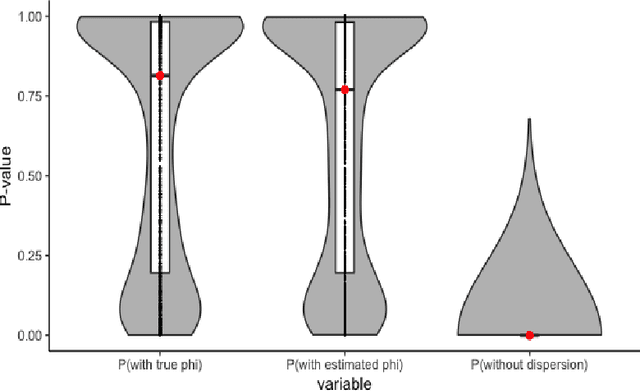

We investigate a general matrix factorization for deviance-based losses, extending the ubiquitous singular value decomposition beyond squared error loss. While similar approaches have been explored before, here we propose an efficient algorithm that is flexible enough to allow for structural zeros and entry weights. Moreover, we provide theoretical support for these decompositions by (i) showing strong consistency under a generalized linear model setup, (ii) checking the adequacy of a chosen exponential family via a generalized Hosmer-Lemeshow test, and (iii) determining the rank of the decomposition via a maximum eigenvalue gap method. To further support our findings, we conduct simulation studies to assess robustness to decomposition assumptions and extensive case studies using benchmark datasets from image face recognition, natural language processing, network analysis, and biomedical studies. Our theoretical and empirical results indicate that the proposed decomposition is more flexible, general, and can provide improved performance when compared to traditional methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge