Determining Structural Properties of Artificial Neural Networks Using Algebraic Topology
Paper and Code
Jan 21, 2021
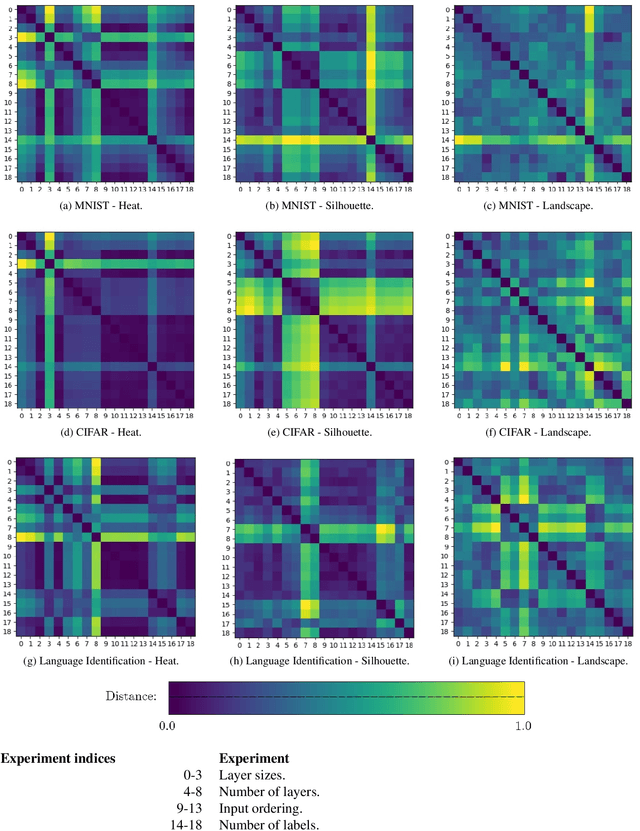
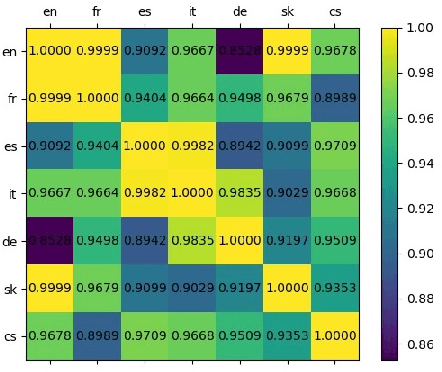
Artificial Neural Networks (ANNs) are widely used for approximating complex functions. The process that is usually followed to define the most appropriate architecture for an ANN given a specific function is mostly empirical. Once this architecture has been defined, weights are usually optimized according to the error function. On the other hand, we observe that ANNs can be represented as graphs and their topological 'fingerprints' can be obtained using Persistent Homology (PH). In this paper, we describe a proposal focused on designing more principled architecture search procedures. To do this, different architectures for solving problems related to a heterogeneous set of datasets have been analyzed. The results of the evaluation corroborate that PH effectively characterizes the ANN invariants: when ANN density (layers and neurons) or sample feeding order is the only difference, PH topological invariants appear; in the opposite direction in different sub-problems (i.e. different labels), PH varies. This approach based on topological analysis helps towards the goal of designing more principled architecture search procedures and having a better understanding of ANNs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge