Designing Rewards for Fast Learning
Paper and Code
May 30, 2022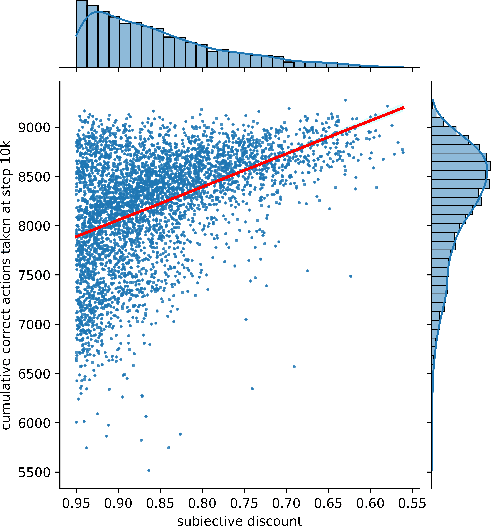
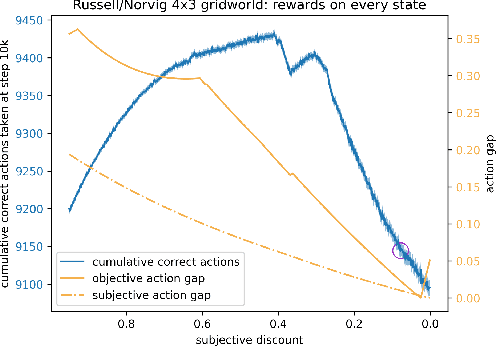
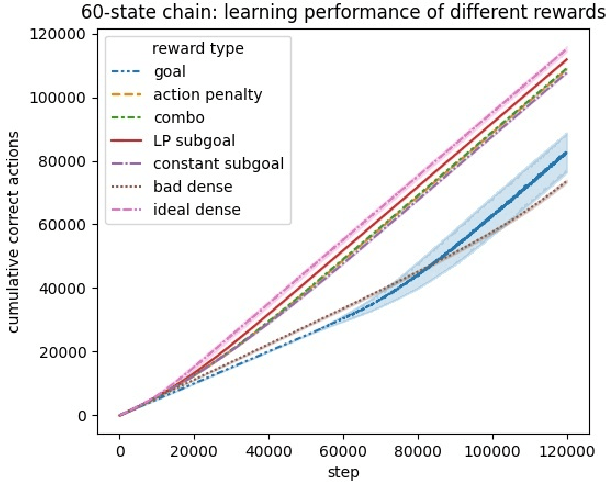
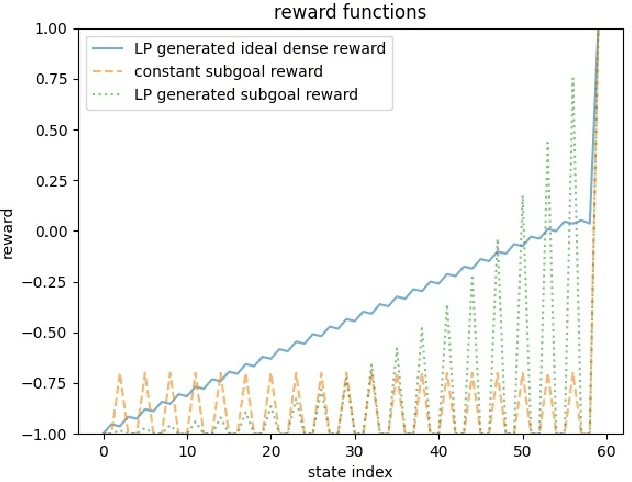
To convey desired behavior to a Reinforcement Learning (RL) agent, a designer must choose a reward function for the environment, arguably the most important knob designers have in interacting with RL agents. Although many reward functions induce the same optimal behavior (Ng et al., 1999), in practice, some of them result in faster learning than others. In this paper, we look at how reward-design choices impact learning speed and seek to identify principles of good reward design that quickly induce target behavior. This reward-identification problem is framed as an optimization problem: Firstly, we advocate choosing state-based rewards that maximize the action gap, making optimal actions easy to distinguish from suboptimal ones. Secondly, we propose minimizing a measure of the horizon, something we call the "subjective discount", over which rewards need to be optimized to encourage agents to make optimal decisions with less lookahead. To solve this optimization problem, we propose a linear-programming based algorithm that efficiently finds a reward function that maximizes action gap and minimizes subjective discount. We test the rewards generated with the algorithm in tabular environments with Q-Learning, and empirically show they lead to faster learning. Although we only focus on Q-Learning because it is perhaps the simplest and most well understood RL algorithm, preliminary results with R-max (Brafman and Tennenholtz, 2000) suggest our results are much more general. Our experiments support three principles of reward design: 1) consistent with existing results, penalizing each step taken induces faster learning than rewarding the goal. 2) When rewarding subgoals along the target trajectory, rewards should gradually increase as the goal gets closer. 3) Dense reward that's nonzero on every state is only good if designed carefully.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge