Dense Limit of the Dawid-Skene Model for Crowdsourcing and Regions of Sub-optimality of Message Passing Algorithms
Paper and Code
Mar 15, 2018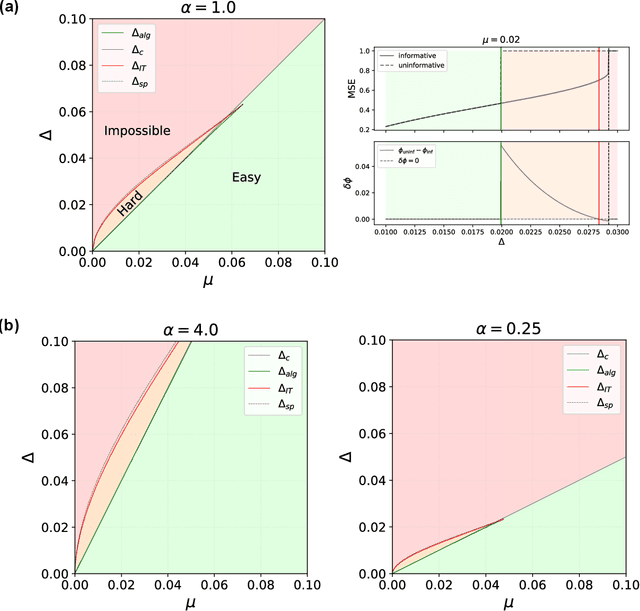
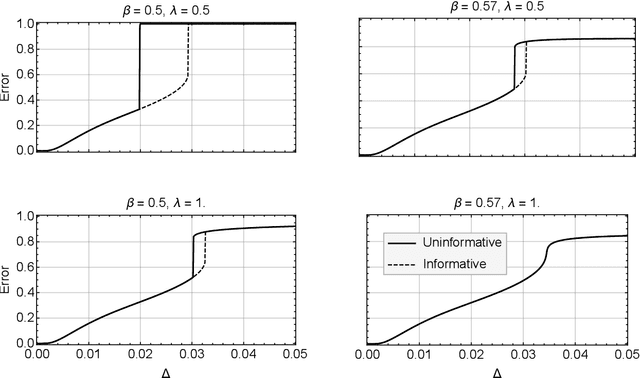
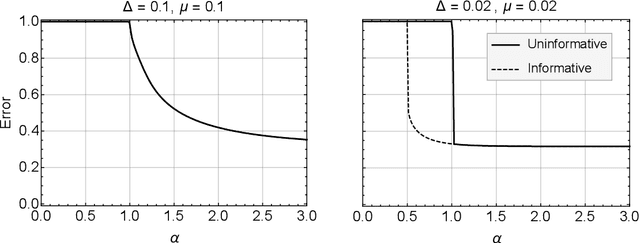
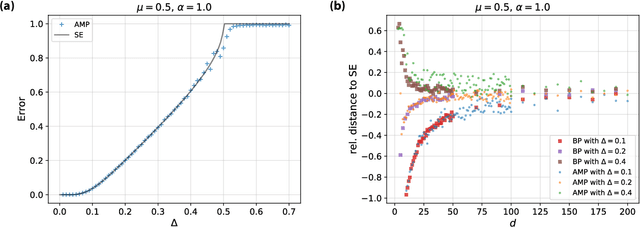
Crowdsourcing is a strategy to categorize data through the contribution of many individuals. A wide range of theoretical and algorithmic contributions are based on the model of Dawid and Skene [1]. Recently it was shown in [2,3] that, in certain regimes, belief propagation is asymptotically optimal for data generated from the Dawid-Skene model. This paper is motivated by this recent progress. We analyze the dense limit of the Dawid-Skene model. It is shown that it belongs to a larger class of low-rank matrix estimation problems for which it is possible to express the asymptotic, Bayes-optimal, performance in a simple closed form. In the dense limit the mapping to a low-rank matrix estimation problem provides an approximate message passing algorithm that solves the problem algorithmically. We identify the regions where the algorithm efficiently computes the Bayes-optimal estimates. Our analysis refines the results of [2,3] about optimality of message passing algorithms by characterizing regions of parameters where these algorithms do not match the Bayes-optimal performance. We further study numerically the performance of approximate message passing, derived in the dense limit, on sparse instances and carry out experiments on a real world dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge