DeltaPhi: Learning Physical Trajectory Residual for PDE Solving
Paper and Code
Jun 14, 2024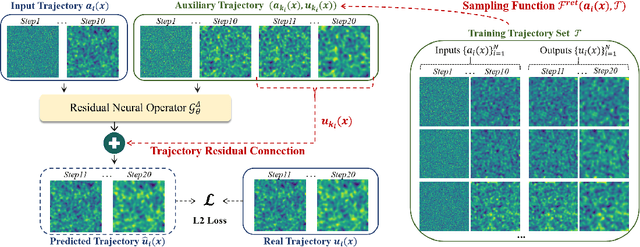
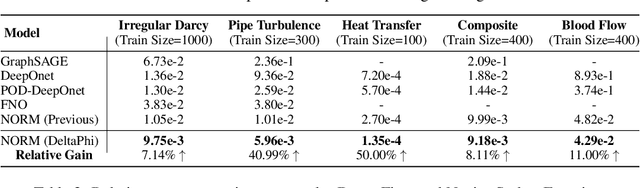
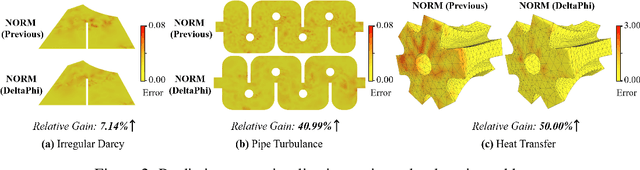
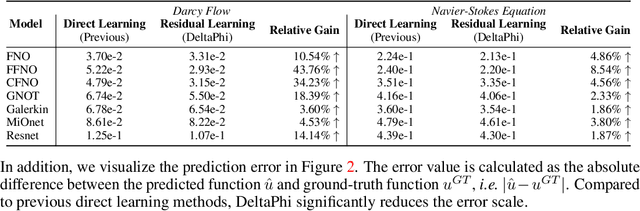
Although neural operator networks theoretically approximate any operator mapping, the limited generalization capability prevents them from learning correct physical dynamics when potential data biases exist, particularly in the practical PDE solving scenario where the available data amount is restricted or the resolution is extremely low. To address this issue, we propose and formulate the Physical Trajectory Residual Learning (DeltaPhi), which learns to predict the physical residuals between the pending solved trajectory and a known similar auxiliary trajectory. First, we transform the direct operator mapping between input-output function fields in original training data to residual operator mapping between input function pairs and output function residuals. Next, we learn the surrogate model for the residual operator mapping based on existing neural operator networks. Additionally, we design helpful customized auxiliary inputs for efficient optimization. Through extensive experiments, we conclude that, compared to direct learning, physical residual learning is preferred for PDE solving.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge