Delayed Geometric Discounts: An Alternative Criterion for Reinforcement Learning
Paper and Code
Sep 26, 2022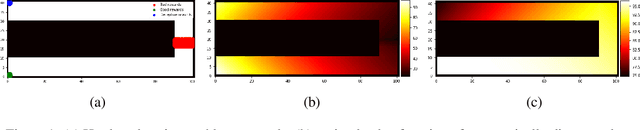

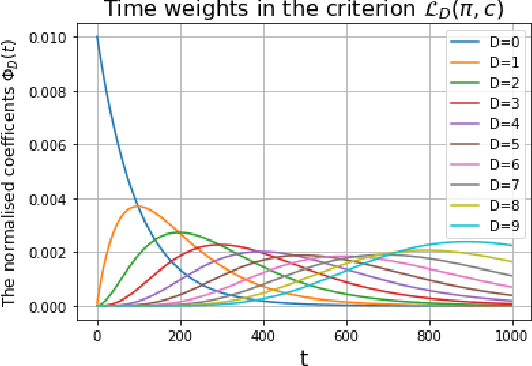
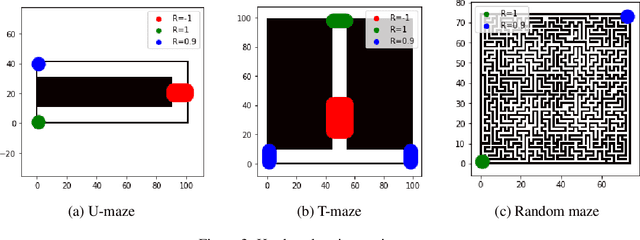
The endeavor of artificial intelligence (AI) is to design autonomous agents capable of achieving complex tasks. Namely, reinforcement learning (RL) proposes a theoretical background to learn optimal behaviors. In practice, RL algorithms rely on geometric discounts to evaluate this optimality. Unfortunately, this does not cover decision processes where future returns are not exponentially less valuable. Depending on the problem, this limitation induces sample-inefficiency (as feed-backs are exponentially decayed) and requires additional curricula/exploration mechanisms (to deal with sparse, deceptive or adversarial rewards). In this paper, we tackle these issues by generalizing the discounted problem formulation with a family of delayed objective functions. We investigate the underlying RL problem to derive: 1) the optimal stationary solution and 2) an approximation of the optimal non-stationary control. The devised algorithms solved hard exploration problems on tabular environment and improved sample-efficiency on classic simulated robotics benchmarks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge