Degree-Preserving Randomized Response for Graph Neural Networks under Local Differential Privacy
Paper and Code
Feb 21, 2022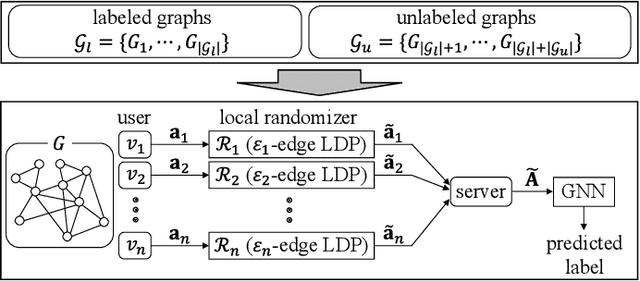
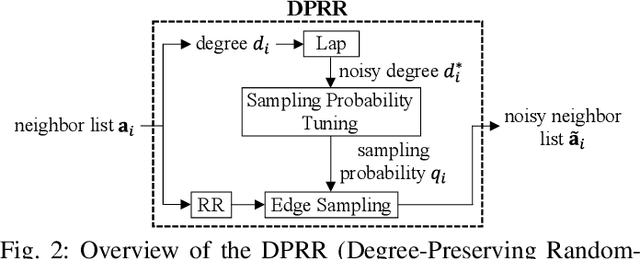
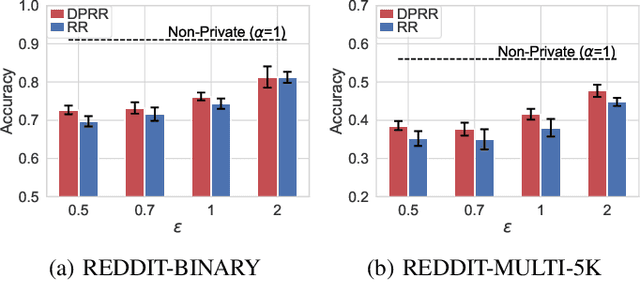
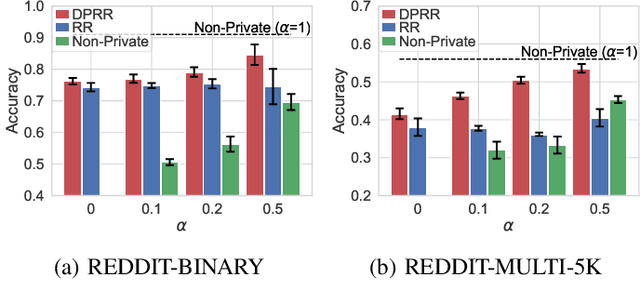
Differentially private GNNs (Graph Neural Networks) have been recently studied to provide high accuracy in various tasks on graph data while strongly protecting user privacy. In particular, a recent study proposes an algorithm to protect each user's feature vector in an attributed graph with LDP (Local Differential Privacy), a strong privacy notion without a trusted third party. However, this algorithm does not protect edges (friendships) in a social graph or protect user privacy in unattributed graphs. It remains open how to strongly protect edges with LDP while keeping high accuracy in GNNs. In this paper, we propose a novel LDP algorithm called the DPRR (Degree-Preserving Randomized Response) to provide LDP for edges in GNNs. Our DPRR preserves each user's degree hence a graph structure while providing edge LDP. Technically, we use Warner's RR (Randomized Response) and strategic edge sampling, where each user's sampling probability is automatically tuned to preserve the degree information. We prove that the DPRR approximately preserves the degree information under edge LDP. We focus on graph classification as a task of GNNs and evaluate the DPRR using two social graph datasets. Our experimental results show that the DPRR significantly outperforms Warner's RR and provides accuracy close to a non-private algorithm with a reasonable privacy budget, e.g., epsilon=1.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge