Deformable Classifiers
Paper and Code
Dec 18, 2017

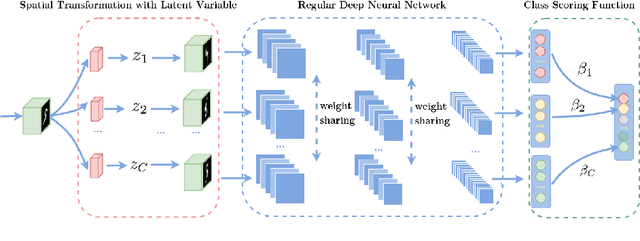
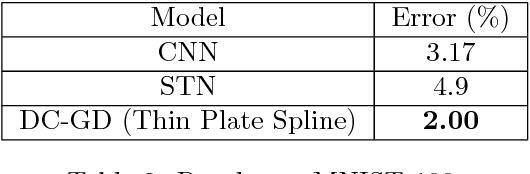
Geometric variations of objects, which do not modify the object class, pose a major challenge for object recognition. These variations could be rigid as well as non-rigid transformations. In this paper, we design a framework for training deformable classifiers, where latent transformation variables are introduced, and a transformation of the object image to a reference instantiation is computed in terms of the classifier output, separately for each class. The classifier outputs for each class, after transformation, are compared to yield the final decision. As a by-product of the classification this yields a transformation of the input object to a reference pose, which can be used for downstream tasks such as the computation of object support. We apply a two-step training mechanism for our framework, which alternates between optimizing over the latent transformation variables and the classifier parameters to minimize the loss function. We show that multilayer perceptrons, also known as deep networks, are well suited for this approach and achieve state of the art results on the rotated MNIST and the Google Earth dataset, and produce competitive results on MNIST and CIFAR-10 when training on smaller subsets of training data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge