Defense Through Diverse Directions
Paper and Code
Mar 24, 2020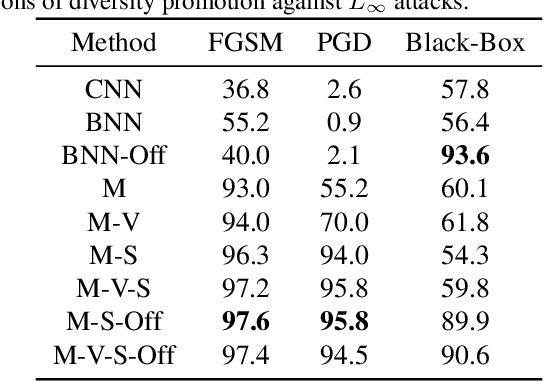

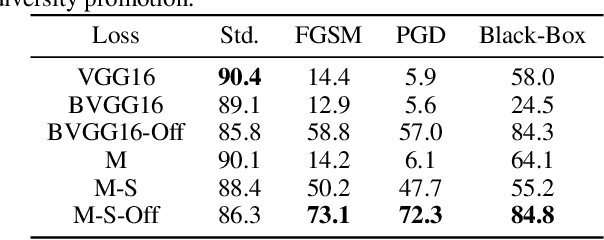

In this work we develop a novel Bayesian neural network methodology to achieve strong adversarial robustness without the need for online adversarial training. Unlike previous efforts in this direction, we do not rely solely on the stochasticity of network weights by minimizing the divergence between the learned parameter distribution and a prior. Instead, we additionally require that the model maintain some expected uncertainty with respect to all input covariates. We demonstrate that by encouraging the network to distribute evenly across inputs, the network becomes less susceptible to localized, brittle features which imparts a natural robustness to targeted perturbations. We show empirical robustness on several benchmark datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge