DeepAveragers: Offline Reinforcement Learning by Solving Derived Non-Parametric MDPs
Paper and Code
Oct 18, 2020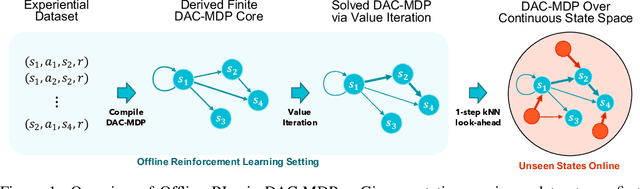
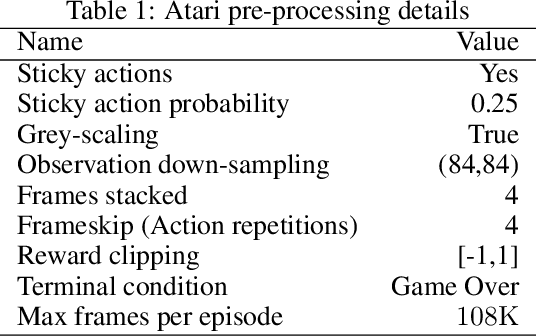
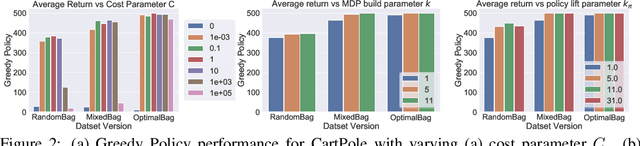
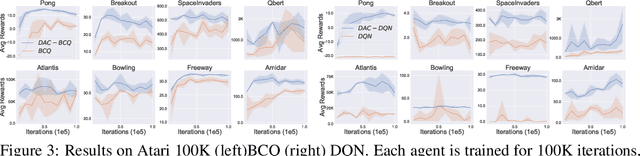
We study an approach to offline reinforcement learning (RL) based on optimally solving finitely-represented MDPs derived from a static dataset of experience. This approach can be applied on top of any learned representation and has the potential to easily support multiple solution objectives as well as zero-shot adjustment to changing environments and goals. Our main contribution is to introduce the Deep Averagers with Costs MDP (DAC-MDP) and to investigate its solutions for offline RL. DAC-MDPs are a non-parametric model that can leverage deep representations and account for limited data by introducing costs for exploiting under-represented parts of the model. In theory, we show conditions that allow for lower-bounding the performance of DAC-MDP solutions. We also investigate the empirical behavior in a number of environments, including those with image-based observations. Overall, the experiments demonstrate that the framework can work in practice and scale to large complex offline RL problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge