Deep Neural Networks are Adaptive to Function Regularity and Data Distribution in Approximation and Estimation
Paper and Code
Jun 08, 2024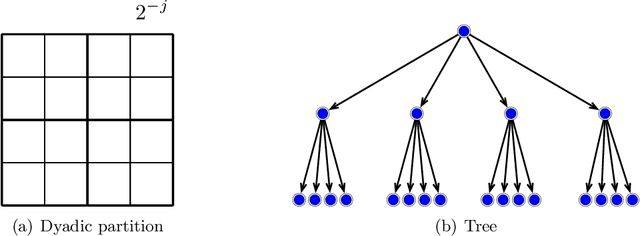
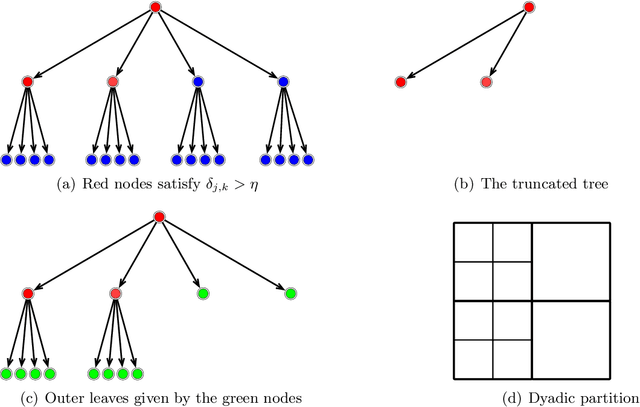
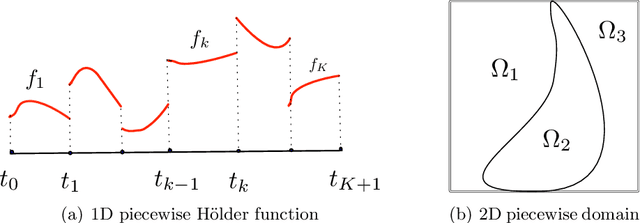

Deep learning has exhibited remarkable results across diverse areas. To understand its success, substantial research has been directed towards its theoretical foundations. Nevertheless, the majority of these studies examine how well deep neural networks can model functions with uniform regularity. In this paper, we explore a different angle: how deep neural networks can adapt to different regularity in functions across different locations and scales and nonuniform data distributions. More precisely, we focus on a broad class of functions defined by nonlinear tree-based approximation. This class encompasses a range of function types, such as functions with uniform regularity and discontinuous functions. We develop nonparametric approximation and estimation theories for this function class using deep ReLU networks. Our results show that deep neural networks are adaptive to different regularity of functions and nonuniform data distributions at different locations and scales. We apply our results to several function classes, and derive the corresponding approximation and generalization errors. The validity of our results is demonstrated through numerical experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge