Deep networks with probabilistic gates

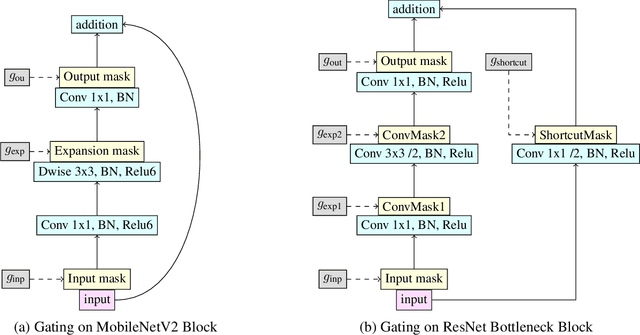
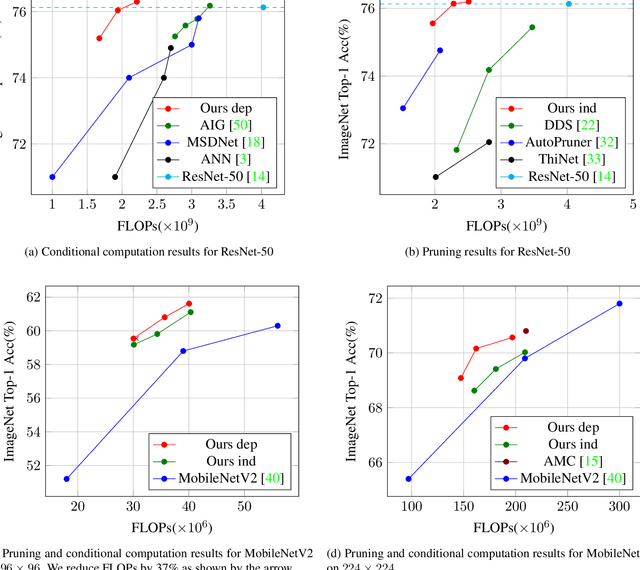
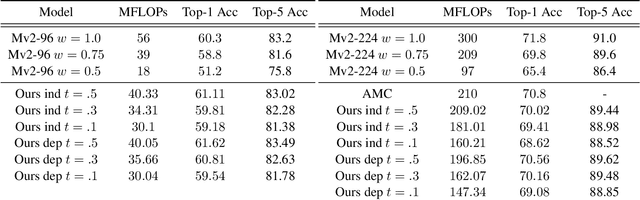
We investigate learning to probabilistically bypass computations in a network architecture. Our approach is motivated by AIG, where layers are conditionally executed depending on their inputs, and the network is trained against a target bypass rate using a per-layer loss. We propose a per-batch loss function, and describe strategies for handling probabilistic bypass during inference as well as training. Per-batch loss allows the network additional flexibility. In particular, a form of mode collapse becomes plausible, where some layers are nearly always bypassed and some almost never; such a configuration is strongly discouraged by AIG's per-layer loss. We explore several inference-time strategies, including the natural MAP approach. With data-dependent bypass, we demonstrate improved performance over AIG. With data-independent bypass, as in stochastic depth, we observe mode collapse and effectively prune layers. We demonstrate our techniques on ResNet-50 and ResNet-101 for ImageNet , where our techniques produce improved accuracy (.15--.41% in precision@1) with substantially less computation (bypassing 25--40% of the layers).