Deep Learning on Implicit Neural Datasets
Paper and Code
Jun 02, 2022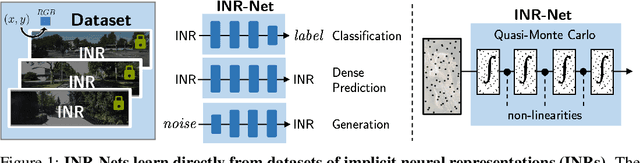

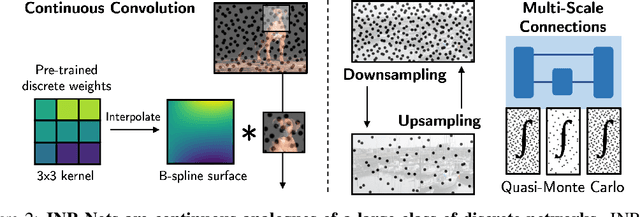
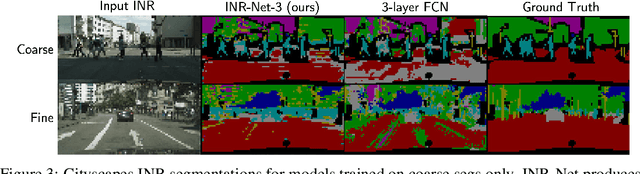
Implicit neural representations (INRs) have become fast, lightweight tools for storing continuous data, but to date there is no general method for learning directly with INRs as a data representation. We introduce a principled deep learning framework for learning and inference directly with INRs of any type without reverting to grid-based features or operations. Our INR-Nets evaluate INRs on a low discrepancy sequence, enabling quasi-Monte Carlo (QMC) integration throughout the network. We prove INR-Nets are universal approximators on a large class of maps between $L^2$ functions. Additionally, INR-Nets have convergent gradients under the empirical measure, enabling backpropagation. We design INR-Nets as a continuous generalization of discrete networks, enabling them to be initialized with pre-trained models. We demonstrate learning of INR-Nets on classification (INR$\to$label) and segmentation (INR$\to$INR) tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge