Deep Learning for Distributed Optimization: Applications to Wireless Resource Management
Paper and Code
May 31, 2019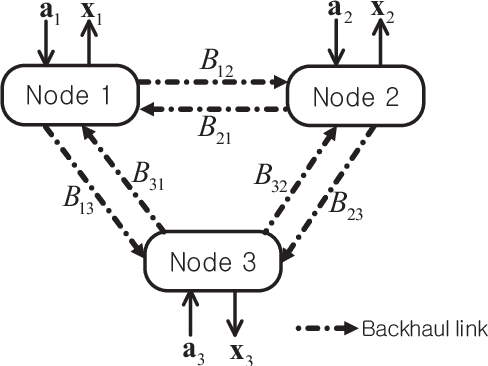
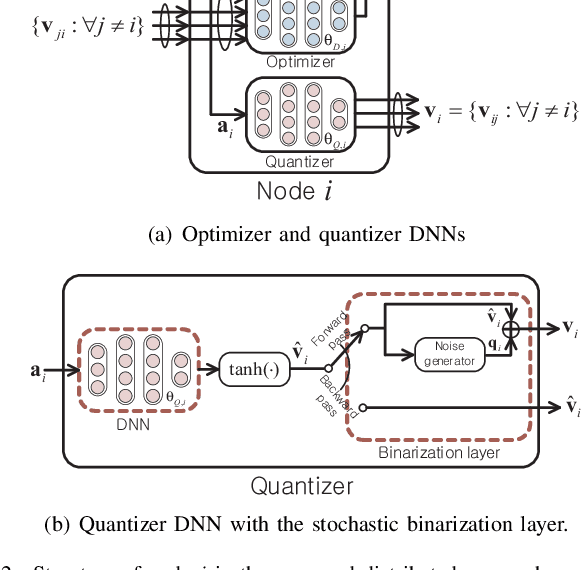
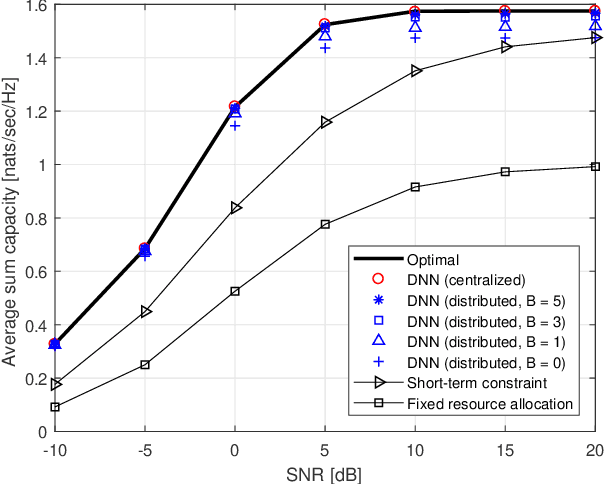
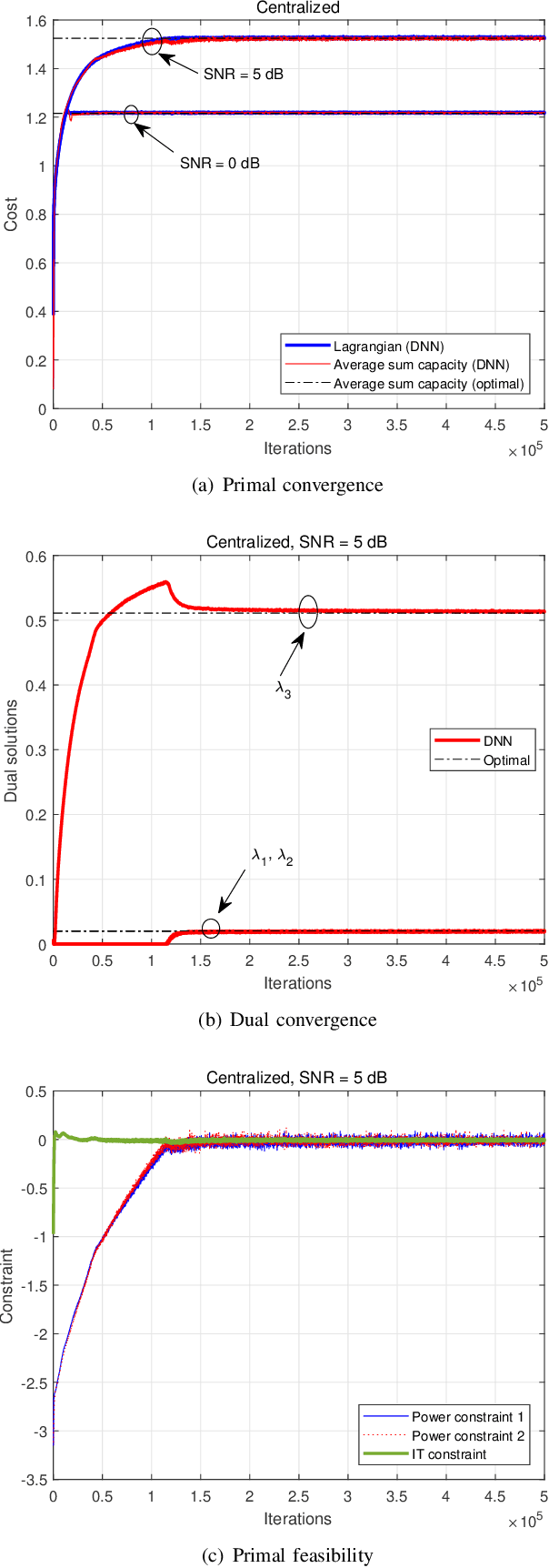
This paper studies a deep learning (DL) framework to solve distributed non-convex constrained optimizations in wireless networks where multiple computing nodes, interconnected via backhaul links, desire to determine an efficient assignment of their states based on local observations. Two different configurations are considered: First, an infinite-capacity backhaul enables nodes to communicate in a lossless way, thereby obtaining the solution by centralized computations. Second, a practical finite-capacity backhaul leads to the deployment of distributed solvers equipped along with quantizers for communication through capacity-limited backhaul. The distributed nature and the nonconvexity of the optimizations render the identification of the solution unwieldy. To handle them, deep neural networks (DNNs) are introduced to approximate an unknown computation for the solution accurately. In consequence, the original problems are transformed to training tasks of the DNNs subject to non-convex constraints where existing DL libraries fail to extend straightforwardly. A constrained training strategy is developed based on the primal-dual method. For distributed implementation, a novel binarization technique at the output layer is developed for quantization at each node. Our proposed distributed DL framework is examined in various network configurations of wireless resource management. Numerical results verify the effectiveness of our proposed approach over existing optimization techniques.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge