Deep Generative SToRM model for dynamic imaging
Paper and Code
Jan 29, 2021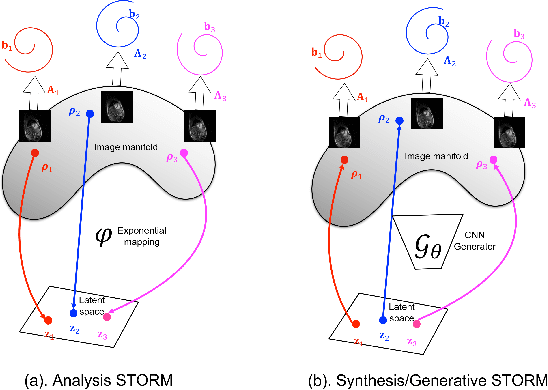
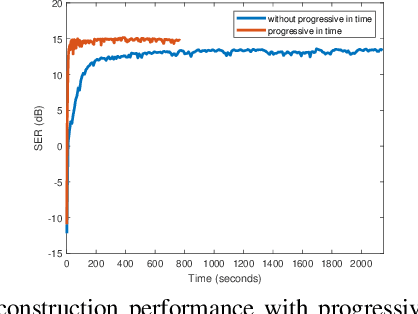
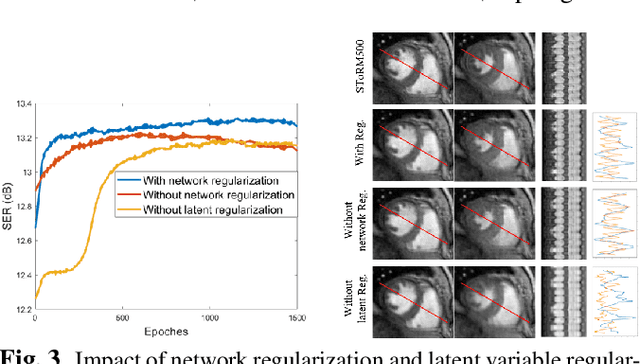
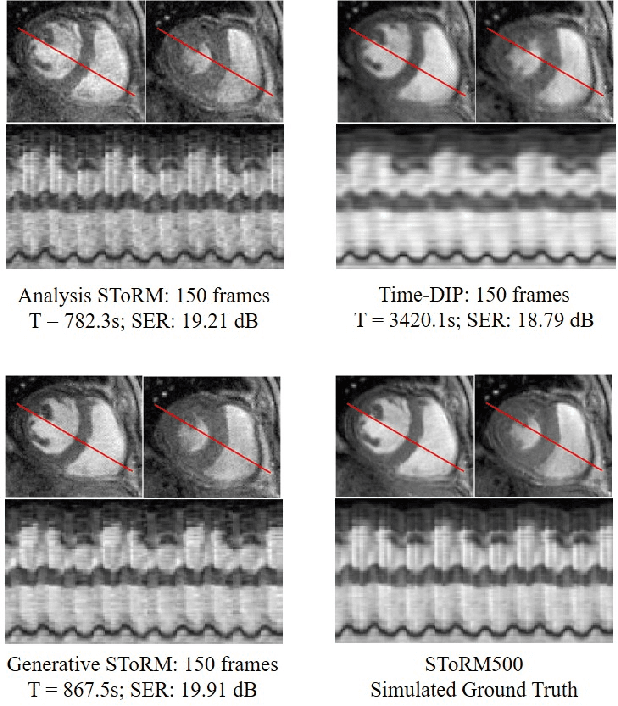
We introduce a novel generative smoothness regularization on manifolds (SToRM) model for the recovery of dynamic image data from highly undersampled measurements. The proposed generative framework represents the image time series as a smooth non-linear function of low-dimensional latent vectors that capture the cardiac and respiratory phases. The non-linear function is represented using a deep convolutional neural network (CNN). Unlike the popular CNN approaches that require extensive fully-sampled training data that is not available in this setting, the parameters of the CNN generator as well as the latent vectors are jointly estimated from the undersampled measurements using stochastic gradient descent. We penalize the norm of the gradient of the generator to encourage the learning of a smooth surface/manifold, while temporal gradients of the latent vectors are penalized to encourage the time series to be smooth. The main benefits of the proposed scheme are (a) the quite significant reduction in memory demand compared to the analysis based SToRM model, and (b) the spatial regularization brought in by the CNN model. We also introduce efficient progressive approaches to minimize the computational complexity of the algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge